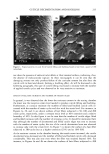
EFFECT OF CURLING IRONS 227 and phase 4, 0%. In all experiments, the hair tresses were combed several times to remove entanglements prior to performing the combing measurements. The combing traces were always collected before and after thermal exposure, and after one or more shampooings as specified in the text of the paper. Subsequently, the effect of treatments was quantified by force-difference combing curves obtained by subtracting untreated control traces from the curves obtained after the treatment. The data are also reported in terms of combing work difference, which represents integrated values of difference combing curves in the region subjected to thermal treatment. The data analysis was performed by employing Microsoft Excel or MathCad software. All combing measure- ments were performed on wet hair. In order to quantify the degree of color changes resulting from heat treatment in various types of hair, we used a HunterLab ColorQUEST sphere spectrocolorimeter manufactured by Hunter Associates Laboratory, Inc., Reston, VA. The use of the spectrocolorimeter enabled us to obtain the tristimulus (oe, •, b) values, which were utilized to calculate discoloration parameters that can be used to describe the adverse effects of thermal treatments. The reported data, in terms of total color difference {AE = •J(AL) 2 + (A•) 2 + (Ab) 2} (Eq.1), chromaticity difference {AC = •/(A•) 2 + (A•) 2} (Eq. 2), and the yellowness index difference (AYI) between unexposed and exposed sections of a hair tress, represent the average of measurements performed at several positions in the designated region on two different tresses. The yellowness index (YI) was calculated using the following equation: 1.28 X- 1.06 Z YI = 100 (Eq. 3) Y where the CIE tristimulus values X, Y, Z are defined as: Y = 0.01 L 2 (Eq. 4) X = 0.9804 0.01 k 2 + 1'-• (Eq. 5) Z-- 1.181 0.01 L2 - •-• (Eq. 6) MATERIALS The majority of the experiments were performed on light-brown hair purchased from International Hair Importers & Products Inc., Valhalla, NY. In order to examine the thermal effects on different types of hair, several experiments were performed on bleached and Piedmont hair purchased from DeMeo Brothers Inc., New York, NY, as well as on Asian and unpigmented (white) hair purchased from International Hair Importers, Inc. Hair tresses were prepared by gluing 2 g of fibers to a 1.5-in x 1.5-in plexiglass tab with Duco Cement. The resulting dimensions of all hair tresses were 6.5 inches in length and 1.25 inches in width. Hair tresses were precleaned with a 3% ammonium lauryl sulfate solution and rinsed thoroughly prior to use in the experiments.

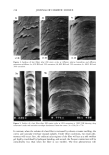
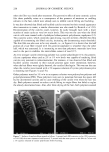
228 JOURNAL OF COSMETIC SCIENCE RESULTS AND DISCUSSION Curling irons are normally applied to dry hair for a short period of time, in the range of 5-20 seconds, at temperatures dependent on the type of hair to be curled. The temperature range of 100ø-120øC is prescribed for very fine or damaged hair, 120 ø- 130øC for fine hair, 130ø-140øC for normal hair in good condition, 140ø-150øC for thick and wavy hair, and 150ø-170øC for coarse, thick, and extremely curly hair. After the application of curling irons, hair is allowed to cool down before combing or brushing or the further application of styling aids. This procedure is frequently repeated several times during the course of a day, resulting in a total treatment time totaling the order of tens of minutes over a time span of a few weeks. In this study we have employed two modes, continuous and intermittent, for the application of curling irons as described in the Experimental section of this report. Using the intermittent mode, each treatment cycle of 15 s was repeated several times for a total treatment time of 3-15 rain, while in the continuous mode the sample was treated continuously for a similar period of time. In order to answer the question on how equivalent these two modes of hair treatment are, in terms of temperature as a function of time and distance within the sample, we have performed theoretical heat-transfer calculations on a model fiber assembly. Equations describing heat transfer for the semi-infinite solid model, proposed by Carlsaw and Jaeger (22), were employed. It was assumed that heat transfer, via conduction, occurs through several layers of fibers in perfect thermal contact with each other. In reality, the fibers would not assume a position of perfect thermal contact, and both the presence of air and water would most likely increase the rate of heat transfer by convection. The physical constants used in the heat transfer calculations, including thermal diffu- sivity values defined by Equation 8 in the Appendix, are displayed in Table I. The parameters characterizing fiber assemblies were calculated as a superposition of the corresponding parameters for hair (79%) and air (21%). In the calculated values for the thermal diffusivity of the fiber, we also account for a 15% water content in the fiber structure, which is approximately an equilibrium amount at room temperature and 65% relative humidity. Figure 2 presents the results of heat transfer calculations through a model fiber assembly characterized by a thickness of 25 fiber layers with a fiber diameter of 70 l•m, i.e., a total thickness of 1750 l•m. The data are plotted in terms of normalized temperature {} (as defined by Equation 9, Appendix) as a function of the dimensionless distance parameter. Table I Parameters Characterizing Thermal Properties/Hair Fiber Assemblies Thermal Conductivity, k Specific heat, c•, Density, p diffusivity, (W/m' K) (J/Kg ' K) (Kg/m 3) (m2/s x 10 Hair fiber* 0.43 (23) 795.492 (24) 1324 (1) 0.04083 Air 0.02624 (25) 1006.3 (25) 1.1769 (25) 2.216 H2 ¸ 0.597 (25) 4181.8 (25) 998.21 (25) 0.0143 Fiber assembly -- 0.497 * The thermal conductivity (k) and specific heat (c•,) values for Polyamide-66 and wool, respectively, were used to represent the constants for a hair fiber.