J. Cosmet, Sci., 52, 185-193 (May/June 2001) Mechanical extension of human hair and the movement of the cuticle M. FEUGHELMAN and B. K. WILLIS, Department of Fibre Science, University of New South Wales, Sydney, NSW 2052 (M.F.), and Reckitt and Colman, P.O. Box 138, West Ryde, Sydney, NSW 2114 (B.K.), Australia. Accepted for publication March 15, 2001. Synopsis Goniophotometry has enabled measurement of the angle that the surface of the cuticle (the scales) of a human hair fiber makes with the axis of the hair shaft. This measuring technique has been used to obtain the change of this scale angle with extension of a hair fiber under fixed conditions of temperature and relative htunidity. Based on a simple model of overlapping scales of the hair cuticle, analysis shows that, for hair fibers extended to strains above 10% at 35% relative humidity and at 35øC, overlapping scales become progressively detached from each other. This scale detachment has been suggested to result from the mechanical failure of the endocuticle layer in the scale structure. This endocuticle layer is low in disulfide cross-linking, which would result in a lowered stiffness and greater extensibility, as indicated by the higher swelling of the layer in water as against the highly cross-linked exocuticle layers. The greater extensibility of the endocuticle would also explain the greater distortion of this layer under stress, but it would not follow that endocuticular failure under stress should result. An alternative mechanism of failure of adhesion between overlapping scales in the cuticle is suggested, based on the involvement of the hydrophobic upper-[3-1ayer with its surface of 18-methyleicosanoic acid (18- MEA), which may provide mobility and a reduction in adhesion between scales. This potential failure of the cementing of the overlapping scale structure due to the 18-MEA is discussed, with particular reference to the standard permanent setting procedure of human hair. INTRODUCTION Stammet aL (1) have studied by means of goniophotometry the specular reflection and the diffuse scattering of light by human hair. The data obtained provided a means of measuring the luster of hair fibers under differing conditions, such as cleanliness of the hair surface, the straightness of the hair and its alignment, and cuticle damage. Fur- thermore, the technique enabled the measurement of the scale angle that the surface of the cuticle (the scales) makes with the axis of the hair shaft. Guiolet et aL (2) have studied the effect of stretching hair on the scale angle. Two series of black and medium bleached hair were examined by them, and both types of hair were found to behave identically, from the point of view of scale angle versus the strain applied. 185

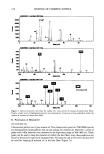
186 JOURNAL OF COSMETIC SCIENCE All these latter measurements were carried out at 35øC and 35% relative humidity. Table 2 in the paper by Guiolet eta/. (2) shows the strain and the corresponding scale angle up to a strain of 33.9%. These results are shown here graphically in Figure 1. Each result is the mean scale angle for 20 fibers at the indicated strain. Although the individual measurements at each strain level fall within a wide range, the general trend of the change of scale angle with strain is clear. In this note the authors examine on the basis of a simple model the scale angle change expected with extension of the hair fiber and its significance in terms of the cuticular scale attachment to the hair fiber main shaft. THE OVERLAPPING SCALE STRUCTURE If no "decementation," mechanical failure, or slippage between overlapping scale struc- tures occurs, the whole cuticle overlay of the fiber will act as a solid as if it were part of the hair cortex. The scale angle versus the longitudinal strain of the fiber is shown in the Appendix to follow Curve B in Figure 1. If slippage between overlapping scales occurs, then the scales will move relative to each other as the hair fiber is extended. Each scale unit is attached directly by its back edge to the hair cortex, and this attachment edge will act as a fulcrum (see Figure 3). The scale angle versus longitudinal strain of the fiber in this latter case is shown in the Appendix to follow Curve A. It should be noted that the thickness of the scales remains unchanged in the calculation of Curve A. If the overlapping scales completely detach from each other, then the scale angle of the extended fiber would be even less affected 3.2 3 2.8 2.6 2.4 0 5 10 15 20 25 30 35 40 •train E• % Figure 1. The plot (x axis) of the relationship between the longitudinal strain, e, applied to a hair fiber (see text) versus the scale angle, 0 (see Figure 3), shown in conjunction with the theoretical curves based on the model shown in Figure 3. Curve A corresponds to the case of free slippage between scales and Curve B to no slippage.