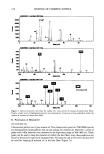
EXTENSION OF HUMAN HAIR 191 ,' Surface of slippage .••'•• betweescale Scale 1- / / ,•C D•• fulcrum at •" • %,,t • Scale 2- B • •.••/O Extension direction,. ,`.,'`.-'`.-'`.-/.•'-/'`.-/.•'-/'`.-'`.-'`.-'`.-'`.-'`.-•'"•'`.-'`.-//////////////////////////////` ,`.,'`.-'`.-'`.-'`.-•'"•.•'-'`.-'`.-'`.-'`.-'`.-.•'-'`.-'`.-'`.-'`.-'`.-.•'-'`.-////////////////////////. ................................................... Hair cortex /////////////////.,,,////////////////////////////////, •'''/•'''/•'''•'''•'''//////////•'''•'''//////////////////////////•'''///•'''//////•'''///////////////////////•'''//////////////////////////////////•'''///• a)///////////.''',.•/,.•/,.•/,.•/.''',.•,.•,.•/,.•,.•/,.•/,.•///,.•///,.•/',.•,.•,.•,.•,.•/,.•/,.•,.•/,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.• ,•caDirection of le rotation '••..-'"/0 •••....0"•0_60 Extension direction . (b) A B B • Figure 3. (a) The model adopted for the movement of two overlapping scales (l and 2) relative to each other and the hair cortex. Each scale is assumed of rectangular section and attached to the hair cortex along a line, which acts as a fulcrum (A and B) for the whole scale (see text). (b) The geometric changes to Scale 2 in 3a with extension of the hair fiber by a strain e. AB will extend to AB' where AB' = (1 + e)AB, and points C• C', D•D'. The angle of the scale to the fiber direction, 0, decreases to (0 - 80) with extension. In all the results quoted in this Appendix, the trigonometric functions of any angle, qb (in radians), is approximated as follows' sin 0 = tan 0 = 0 and

192 JOURNAL OF COSMETIC SCIENCE cos 0: 1 because all angles quoted are less than 3 ø (0.5236 radians), and sin 3 ø = 0.5234, tan 3 ø -- 0.5241, and cos 3 ø = 0.9986. From equation 3, sin(f} - 8f}) = sin f} cos (8f}) - cos f} sin(Bf}) which reduces, on application of the approximations indicated above, to sin(f} - 8f}) = sin f} - 8f} = f}-sf} (4) Inserting equation 4 into equation 3 reduces to (• + •) (0- 80): 0 0 -1 +e (5) Although 0 and 50 were expressed in radians, because is 50/0 is a ratio, equation 5 is independent of the units of the values of 0 and 80 and holds for the values of the angles expressed in degrees. This is the case in Figure 1 for Curve A: the relationship between the scale angle and the strain • on the fiber is given by equation 5, with both 0 and 80 expressed in degrees. Where there is complete adherence between the scales, the whole cuticle structure acts as a solid and as a part of the underlying cortex of the fiber. The result of an extension of the hair fiber by a strain • is a lateral compression strain of ty• where ty is the Poisson ratio of the scale material. The result is that the scale angle changes with an extension strain • due to the value of AB going to AB' and DB to D'B'. As in equation 1 AB' : (1 + •)AB (6) However, due to the lateral strain on the fiber D'B' = DB(1 - rye) (7) and with the scale thickness no long constant DB = AB tan 0 = AB(0) (8) and D'B' = AB' tan(0 - which approximates with equation 6 to D'B' = (1 + e)AB(0 - 80) Inserting equations 7 and 8 into equation 9 and approximating tan 0 = 0, (9) O(1 - try) = (• + •)(0 - 80) (•0)