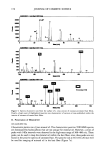
190 JOURNAL OF COSMETIC SCIENCE combing and brushing will not remove the last layer of cuticle cells for some consid- erable time and thus for the length of hair. However, the amount of 18-MEA per unit length of hair would progressively decrease until the last cuticle layer is removed, exposing the hair cortex, leading to subsequent breakup of the fiber end. The action of cationic conditioners serves to replace the lubricating surface where 18-MEA has been depleted, helping to preserve the cuticle layer for substantially greater lengths of hair. Unlike the 18-MEA layer, conditioners are not covalently bonded to the cuticle surface and need to be replaced after the hair is washed to retain the lubricating action and protective effect. APPENDIX The overlapping scales, which form the cuticular outer layer of a human hair fibers, are attached by their inner edge to the hair cortex, the main shaft of the fiber. The over- lapping scales form a serrated system of scale edges on the surface of the cuticle. For the purposes of this analysis the scales are considered as platelets rectangular in cross section and capable of rotation about a line fulcrum (A and B in Figure 3a,b). With the fiber unextended, the angle of the scales to the direction of the fiber is 0. If the fiber is extended by strain e, the attachment of scales to the main shaft (A and B in Figure 3a, b) will move apart, and the scale angle, 0, will reduce to (0-80). The dotted scale in Figure 3b represents the changed position of Scale 2 after extension, and AB' = (1 + e)AB (1) In Figure 3b, BC is perpendicular to the Scale 2 surface with the fiber unextended and B'C' with the fiber extended. Similarly, BD is perpendicular to AB, and B'D' is perpendicular to AB'. The thickness of the scale, t, is for the unextended fiber. With low adherence between overlapping scales, extension of the fiber will result in slippage between scales, as indicated in Figure 3a. The thickness, t, of the scales will remain unchanged because of the negligible lateral forces transferred between the scales. In the unextended state, the scale thickness, t, is given by t=BC = AB sin 0 (2) If slippage occurs between the scales on extension of the fiber and the thickness remains unchanged, then BC = B'C' = t It follows that because then That is, from equation 1 B'C' -- AB' sin(0 - 80) AB' sin(0 - 80) = AB sin 0 (1 + e)sin(0 - 80) = sin 0 (3)

EXTENSION OF HUMAN HAIR 191 ,' Surface of slippage .••'•• betweescale Scale 1- / / ,•C D•• fulcrum at •" • %,,t • Scale 2- B • •.••/O Extension direction,. ,`.,'`.-'`.-'`.-/.•'-/'`.-/.•'-/'`.-'`.-'`.-'`.-'`.-'`.-•'"•'`.-'`.-//////////////////////////////` ,`.,'`.-'`.-'`.-'`.-•'"•.•'-'`.-'`.-'`.-'`.-'`.-.•'-'`.-'`.-'`.-'`.-'`.-.•'-'`.-////////////////////////. ................................................... Hair cortex /////////////////.,,,////////////////////////////////, •'''/•'''/•'''•'''•'''//////////•'''•'''//////////////////////////•'''///•'''//////•'''///////////////////////•'''//////////////////////////////////•'''///• a)///////////.''',.•/,.•/,.•/,.•/.''',.•,.•,.•/,.•,.•/,.•/,.•///,.•///,.•/',.•,.•,.•,.•,.•/,.•/,.•,.•/,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.•,.• ,•caDirection of le rotation '••..-'"/0 •••....0"•0_60 Extension direction . (b) A B B • Figure 3. (a) The model adopted for the movement of two overlapping scales (l and 2) relative to each other and the hair cortex. Each scale is assumed of rectangular section and attached to the hair cortex along a line, which acts as a fulcrum (A and B) for the whole scale (see text). (b) The geometric changes to Scale 2 in 3a with extension of the hair fiber by a strain e. AB will extend to AB' where AB' = (1 + e)AB, and points C• C', D•D'. The angle of the scale to the fiber direction, 0, decreases to (0 - 80) with extension. In all the results quoted in this Appendix, the trigonometric functions of any angle, qb (in radians), is approximated as follows' sin 0 = tan 0 = 0 and