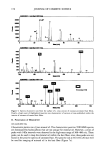
192 JOURNAL OF COSMETIC SCIENCE cos 0: 1 because all angles quoted are less than 3 ø (0.5236 radians), and sin 3 ø = 0.5234, tan 3 ø -- 0.5241, and cos 3 ø = 0.9986. From equation 3, sin(f} - 8f}) = sin f} cos (8f}) - cos f} sin(Bf}) which reduces, on application of the approximations indicated above, to sin(f} - 8f}) = sin f} - 8f} = f}-sf} (4) Inserting equation 4 into equation 3 reduces to (• + •) (0- 80): 0 0 -1 +e (5) Although 0 and 50 were expressed in radians, because is 50/0 is a ratio, equation 5 is independent of the units of the values of 0 and 80 and holds for the values of the angles expressed in degrees. This is the case in Figure 1 for Curve A: the relationship between the scale angle and the strain • on the fiber is given by equation 5, with both 0 and 80 expressed in degrees. Where there is complete adherence between the scales, the whole cuticle structure acts as a solid and as a part of the underlying cortex of the fiber. The result of an extension of the hair fiber by a strain • is a lateral compression strain of ty• where ty is the Poisson ratio of the scale material. The result is that the scale angle changes with an extension strain • due to the value of AB going to AB' and DB to D'B'. As in equation 1 AB' : (1 + •)AB (6) However, due to the lateral strain on the fiber D'B' = DB(1 - rye) (7) and with the scale thickness no long constant DB = AB tan 0 = AB(0) (8) and D'B' = AB' tan(0 - which approximates with equation 6 to D'B' = (1 + e)AB(0 - 80) Inserting equations 7 and 8 into equation 9 and approximating tan 0 = 0, (9) O(1 - try) = (• + •)(0 - 80) (•0)

EXTENSION OF HUMAN HAIR 193 which reduces to - -- (11) 0 1+• In amorphous solids •r approximates to 0.5, and equation 11 can be reduced to 80 3e 0 -2(1 + •) (12) Equation 12 corresponds to Curve B in Figure 1, the relationship between scale angle and strain when there is complete attachment and no slippage between scales. ACKNOWLEDGMENTS The authors would like to acknowledge Dr. Heather Patrick for her help in preparing the manuscript. REFERENCES (1) R. F. Stature, M. L. Garcia, and J. J. Fuchs, The optical properties of human hair. Parts I, II, J. Soc. Cosmet. Chem., 28, 571-599, 601-609 (1977). (2) A. Guiolet, J. C. Gatson, and J. L. Levecque, Study of optical properties of human hair, Int. J. Cosmet. Sci., 9, 111-124 (1987). (3) M. Gamez-Garcia, Cuticle decementation and cuticle buckling produced by Poisson contraction on the cuticular envelope of human hair, J. Cosmet. Sci., 49, 213-222 (1998). (4) J. A. Swift, Human hair cuticle: Biologically conspired to the owner's advantage, J. Cosmet. Sci., 50, 23-47 (1999). (5) S. B. Ruetsch, and H. D. Weigmann, Mechanism of tensile stress release in the keratin fiber cuticle. I.,J. Soc. Cosmet. Chem., 47, 13-26 (1996). (6) L. N. Jones, and D. E. Rivett, The role of 18-methyleiconosanoic acid in the structure and formation of mammalian hair fibers, Micron, 28, 469-485 (1997). (7) V. Robinson, in Mechanical Properties and Structure of Alpha-Keratin Fibres, M. Feughelman, Ed. (Uni- versity of New South Wales Press, Sydney, Australia, 1997), p. 4. (8) J. A. Swift, Fine details on the surface of human hair, Int. J. Cosmet. Sd., 13, 143 (1991). (9) L. N. Jones, D.J. Peet, D. M. Danks, A. P. Negri, and D. E. Rivett, Hair from patients with maple syrup urine disease shows a structural defect in the fibre cuticle, J. Invest, Dermatol., 106, 461-464 (1996). (10) V. Robinson and S. Kelly, The effect of grooming on the hair cuticle, J. Soc. Cosmet. Chem., 33, 203-215 (1982). (11) M. Feughelman, A note on the permanent setting of human hair, J. Soc. Cosmet. Chem, 41, 209-211 (1990).