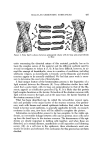
428 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS 1.2 per cent longitudinally. Equally, there are changes in the torsional- longitudinal modules ratio (9, 16). The two-phase model is one in which a system of rodlets or fibrils, hydro- phobic in nature, are imbedded in an amorphous hydrophilic matrix. Water entering this system affects the hydrogen and salt bonds of the matrix, while the rodlet-fibrils remain relatively unaffected. The swelling experiments bear this out: the rapid rate of radial swelling is indicative of matrix bond break- down, while the low rate of longitudinal swelling is indicative of the fibril sys- tem molecular stability. A reduction in the longitudinal Young's Modulus is indicative of a change in the summation of the fiber matrix relationship, con- tributing to the total elasticity (3, 7, 9, 16). These changes are caused by variance in the water content of the fiber as a result of varied relative humidity. Water, in effect, is used as a model condi- tioning agent for the purpose of these experiments. Within the realm of cosmetic conditioning and treatment, there also exist more severe agents (i.e., permanent waving solutions and bleaches), which not only affect the hydrogen and salt linkages, as is the case with water, but also the disulphide and even, at the extreme, the fibril backbone peptide bonds. These agents also have an effect equal in magnitude on the two-phase system and ultimately the mechanical-physical properties of hair (1, 7, 20). This two-phase mechanical model has a rather unique correlation: it emerges surprisingly similar to the classic Frey-Wyssling optical model of composite body-rodlet birefringence (Fig. 15) (19). In this model, rodlet or miceIlar structures of a crystalline nature are imbedded in a surrounding medium of a different refractive index, as is the case in hair. The rodlet struc- tures themselves are responsible for a contribution to the birefringence of the total system in the mode of intrinsic birefringence. In addition, however, the relationship between the refractive index of the rodlets and their surrounding medium produces form birefringence, which is directly proportional to the difference between the 2 refractive indices of the components. The summa- tion of intrinsic and form birefringence equals the total: numerical birefrin- gence (3, 4, 11 19). In Table I, the significance of a numerical birefringence system to deter- mine the static condition of a hair strand can be seen. Previous work corre- lating the molecular orientation .of fibrous material, as measured by numeri- cal birefringence, with sonic pulse velocity, which is very well correlated with Young's Modulus in hair, encourages this (9.1, 9.2). The correlation matrix explains the contributions of the various parameters to the dependent vari- able, grams force at 10 per cent deformation, as well as any interactions which occur berween parameters. Cross-sectional area offers the greatest single con- tribution to the force a large hair is expected to require more force than a small one. In addition, information a•bout the orientation or integrity of the

POLARIZATION MICROSCOPY 41•9 Figure 15. C],assical Frey-Wyssling optical model of composite body-rodlet birefring- ence [with permission of the publisher (19)] fiber-matrix system can be sought from the numerical birefringence value. This correlation, however, is low and not significant. (It does not appear in the solution vector. ) This is due to the inherent characteristics of human hair be- ing such that the numerical birefringence has a tendency to be inversely pro- portional to the cross-sectional area (the correlation of parameters 2 with 1) and, thus, is not independent. In order to get additional information about orientation and integrity, the interaction term of the cross-sectional area and numerical birefringence must be looked at to correct for nonindependence. This parameter has a correlation of 0.85 with the grams force. The solution vector is based upon the 143 hairs placed into the model. It can be seen by the statistical t-values that the 2 parameters, area and the in- teraction of area and numerical birefringence, are highly significant: P 0.01.