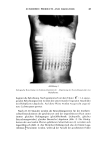
ANTIFOAMS 109 z z ¸ z SCHEMATIC REPRESENTATION OF ENERGY PROFILE DURING FOAM THINNING EE / / ,, / • /- DISTANCE OF /' /ET TM • SEPARATION, Figure 1. Variation in the interactive energies on approach of two bubbles. Curve 1 shows a net positive energy barrier Curve 2 does not. external factors or of local thermal motions which can cause fluctuations in the film thickness to or below the critical rupture thickness, hr. The actual stability of the foam and the values of h e and h• are dependent on (a) the interfacial packing density of the stabilizing surfactant and (b) the nature, size and configuration of its polar group. The rate of film thinning depends directly upon the magnitude of the driving energy and inversely upon the bulk and surface viscosities. In particular, the role of surface viscosity becomes significant when appreciable film thinning has already occurred. Even nonpersistent foams can demonstrate remarkable stability by virtue of having very slow film drainage characteristics. This is particularly true for foams where the surface and/or bulk exhibit non-Newtonian behavior such that the viscosity increases sharply with a decrease in the shear rate or the drainage rate. Under these conditions, even though film thinning is favored energetically, the slow kinetics of thinning impart appreciable stability to the foam. These types of foam are expected to be encountered with nonionic surfactants or polymers in aqueous solutions or, in general, in nonaqueous media, where electrical repulsive forces play a limited role.

110 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS The discussion so far has suggested that there are several conditions under which one can expect to produce foams with indefinite stability. These are, however, seldom encountered because there are, in addition, several factors which can cause local fluctuations in the film thickness, resulting in force imbalances and consequent film rupture. These factors include: (1) evaporation of the liquids, (2) gas diffusion and corresponding changes in the size and size distribution of the bubbles, (3) thermal motions, (4) mechanical disturbances, (5) interactions involving the absorption of sound or electromagnetic radiation and (6) local compositional fluctuations. Foams derive stability against such local fluctuations by their ability to resist thinning and their ability to heal weak spots. Surface viscosity and surface elasticity are two primary properties which enable a foam to restore itself and resist rupture from local stressing. Gibbs' surface elasticity is defined as: e = 2d3'/d In A •- -- 2P (d3'/dP) where 3' is the surface tension of the foaming solution, A is the area per molecule of the surfactant, and I' its adsorption density, at the interface. The higher e, the higher the restoring force to a local surface concentration fluctuation and, hence, the higher will be the film stability. Mechanistically, this implies that any external perturbance which either dilates or contracts the surface film, i.e., decreases or increases the surfactant adsorption density, will be opposed by a corresponding change in surface tension thereby minimizing the effect of the perturbance. These aspects have been dealt with in some detail by Mysels (3). However, direct proof is limited owing to experimental diflSculties. A high level of surface viscosity or viscoelasticity represents another factor affecting film stability by its influence on film drainage. A higher surface viscosity implies a lower rate of liquid drainage within the lamellae and the movement of a layer of subsurface solution during the healing of a locally thinned film. Films with viscoelastic properties will, in addition, stabilize foams because film thinning can be practically stopped owing to the high restoring force accompanying a local displacement together with a reduction in drainage rates. The latter is especially significant when the shear stress, due to the drainage, falls below the yield stress of the film. Scheludko (6) postulated that the film rupture is caused by surface ripples which are generated primarily by thermal motion. He derived an expression for the critical thickness, hr, which a single film must reach before rupture can occur. Vrij (7), by light scattering experiments, found evidence of such fluctuations and modified Scheludko's equation for hr, obtaining the expressions {A ro• •/4 = ] when E v • • EH and IA 2 r hr = 0.267[-- •o / \f3' when E H • • E v. Here r o is the radius of the single film, A and 3' are the Hamaker constant of the film and its surface tension, respectively, and f is a parameter, depending on H and 3', which decreases with thickness.