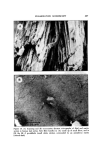
J. Soc. Cosmet. Chem., 27, 411-431 (September 1976) Birefringence: Polarization Microscopy as a Quantitative Technique of Human Hair Analysis ROGER K. CURTIS, B.A. and DON R. TYSON, B.S.* Presented May 29, 1975, SCC Seminar, St. Louis, Missouri Synopsis: An alternative to the conventional met•hod of mechanical stress-strain analysis of HUMAN HAIR condition is presented in this paper. NUMERICAL BIREFRINGENCE is an extremely sensitive measure of molecular orientation. As such, this technique has the potential of determining hair fiber condition at a fundamental molecular level. Basic theories of POLARIZATION MICROSCOPY are presented and utilized as the basis of a qtmntitative technique developed for the measurement of birefringence in hair. The theories, morphological origins, and contributions of both the intrinsic and form bire- fringence components, and the correlation of numerical birefringence with the mechanical properties of hair are discussed. Numerical birefringence, a quantitative measure of the optical anisotropic properties of a hair fiber cortex, as a reflection of the hair strand condition presently observed with mechanical stress-strain testing, is demonstrated. INTRODUCTION The traditional method of detemining the condition of a human hair fiber is by measuring its mechanical stress-strain characteristics. The parameters determined, including: Young's modulus force at yield point ultimate tensile s•rength and either break point extension, or various parameters of elastic recovery hysteresis (1) are abstract or secondary effects of the basic chemi- cal-molecular occurrences in cosmetic treatment and conditioning. Wha• is needed is an additional system oi analysis, which by looking at hair on a foun- dation molecular level, is more specific. Crystalline, or molecular chain-sheet substances of a nonisometric nature, exhibit the optical property of birefringence when they are placed in a field oi plane polarized light (2). This phenomenon, due •o a condition known as *Redken Laboratories, Inc., Van Nuys, California 91411. 411
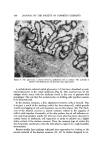
412 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS optical anisotropism, is a result of electron orbit polarizability and/or a re- fraetive index differential between a crystal and its surrounding medium in which the crystal is embedded (2, 3, 4). The quantitative measure of bire- fringence, referred to as the numerical birefringence, is an extremely sensitive measure of optical anisotropism, wh'ch arises from molecular orientation 5). The cortical region of a human hair is optically anisotropic (3, 6). In its function as the maior fiber component (7), the cortex contributes 92 per cent to the elasticity of the hair. This is borne out by an analysis of the correlation matrix of a multiple linear regression model that explains the factors con- tributing to elasticity in hair (8, 14). In the course of a cosmetic treatment, be it chemical or mechanical in nature, the condition of a hair fiber is changed. The parameter of elasticity, or the resistance to and recovery from deformation by force, plays a maior role in the final fiber condition after treatment(1). The change of condition during cosmetic treatment is due to molecular bonding changes, which occur mainly in the cortex (7, 9). Therefore, the action of cosmetics, which affect condition and elasticity, should also affect the optical anisotropism of the cortex. Thus numerical bire- fringence, as a very sens:tive measure of molecular orientation, emerges as having the potential to very accurately determine hair condition. This paper presents a quantitative system of analysis of human hair condi- tion, based upon the optical phenomenon of numerical birefringence. Theory of Bitefringe Plane polarized light is utilized to observe the phenomenon of birefrin- gence. Ordinary light vibrates in waves, traveling in random planes perpen- dicular to the direction of propagation. By placing a polarization plate in front of a light soume, only those waves tarveling in planes parallel to the axis of polarization of the plate are transmitted the others being absorbed (Fig. 1A). An anisotropic material has two unique optical properties as follows: (1) any one plane of light waves striking an anisotropic material is split into two wave-planes, traveling 90 ø relative to each other and 45 ø each relative to the original plane of propagation (Fig. i B). Hence the term double refraction or birefringence (2) a plane of light passing through an anisotropic material encounters a path of a different refractive index, and thus travels at a different veloc'ty, in each different direction of traverse (2, 5). Therefore, a wave of plane polarized light strikes an anisotropic material, is split into two waves, one of which, the ordinary or simply fast wave, is travel- ing through a path of lesser refractive index, and thus faster than the extra- ordinary or slow wave, which is traveling at a perpendicular angle in a more difficult path of higher refractive index (2, 5).
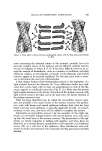
Purchased for the exclusive use of nofirst nolast (unknown) From: SCC Media Library & Resource Center (library.scconline.org)