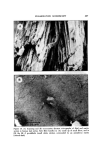
POLARIZATION MICROSCOPY 413 ORDINARY LIGHT AND PLANE POLARIZED LIGHT AXIS OF POLARIZATION ORDINARY LIGHT ' POLARIZER PLANE POLARIZED LIGHT DIRECTION Of PROPAGATION PLANE POLARIZED LIGHT PASSING THROUGH AN ANISOTROPIC MEDIUM FAST WAVE ANISOTROPIC WAVE MEDIUM 2 WAVE PLANES 90 ø TO EACH OTHER 45 ø EACH TO THE PLANE POLARIZED LIGHT Figure 1. (A) Ordinary light waves being polarized and (B) ordinary light waves further split into two perpendicular waves, each traveling at different velocity, while travers- ing anisotropic medium The difference in refractive index between the two paths of the fast and slow wave (n,o-nl) equals the numerical birefringence (2). As the 2 waves advance through the material, the slow wave increasingly lags behind the fast wave in direct proportion to the numerical birefringence (the difference in path velocities) and to the distance or thickness traveled. This quantity of "lag," measured in units of distance, is termed retardation. Hence the formulation, retardation equals numer_'cal birefringence x thick- ness or A= (n2-nl)d. The numerical birefringence is determined by measuring the retardation and the thickness (2). The retardation lag of the slow relative to the fast wave causes the two waves to go out of phase with each other (Fig. 2). These two waves, exiting the anisotropic material, interfere with each other, causing an elliptical interference pattern. In Fig. 3(A) the two waves are coming at you in phase with each other, the retardation distance having been some full multiple of the wavelength (A = nX). They are vibrating in unison, i.e., each reaching points 1-20 at the same time from points A, A' to B, B'. The elliptical inter- ference pattern is centered around an axis, formed by connecting the points of intersection of consecutive lines, drawn from the wave position at a particular instant, perpendicular to the wave axis. In Fig. 3 (B), the slow wave has been

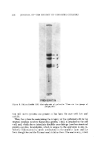
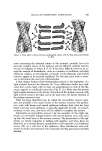
414 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS INCREASING RETARDATION OF THE SLOW RELATIVE TO FAST WAVE WAVE s,ow/w-,, WAVE / •,,_//•, _'g,X RETARDED (IN PHASE) \_/ k../ / 1/4 ),RETARDED 1/,, X RETARDED 1 ),RETARDED ('IN PHASE] DIRECTION OF RETARDATION •' DIRECTION OF TRAVEL Figure 2. Two parallel waves of equal length X, traveling different velocities. As slow wave increasingly retards from fast wave, two go in and out of phase with each other • ELLIPTICAL /I" RESULTANT /•""• INTERFERENCE / ELLIPTICAL •, /•AXIS • 1 INTERFERENCE • / PATTERN • /(NEGATIVE IMAGE) • • /•• ., ( • • t •J •" • AXIS OF POLARIZATION '••'• I •• • ..•/_•• • •{gure 3. Ode•t•tJo• o• e]]•tJe•] J•te•e•egee •tte• •o•me• by two J•te•ed•g w•ves (A) • p•ase a• (•) ¾2 X o.t o• p•se (see tezt) retarded some full multiple of the wavelength plus one-half (A = n + 1/2X). In this case, as the fast wave advances from point A, through points 1-20, finally to point B, the slow wave, being 1/2X out of phase, advances from point