643 Address all correspondence to Duane Harland, duane.harland@agresearch.co.nz What Causes Curly Hair? MARINA RICHENA AND DUANE P. HARLAND AgResearch, Lincoln, New Zealand (M.R., D.P.H.) Synopsis We do not know what causes natural-born curliness in human scalp hair or in the hair of mammals in general. This brief review describes why hair curls, and the cause of the phenomenon is more complex than often appreciated. We then briefly review features that are associated, correlated, or purportedly cause hair curl. INTRODUCTION “Eat up your bread crusts children, so that your hair grows curly.” —Traditional This old British saying was more about food wastage than hair. However, crusts aside, the causes of and influences on hair curl are still not completely understood. Here we briefly review current work in this area and explain why answering the deceptively simple question of “what causes curl” remains a challenge. WHY DO WE CARE? We notice hair. Lack of hair, color, texture, and style of hair provide visual information from which our brains subconsciously extract useful social information, such as individuality and conformity to norms. Hair is a tricky signal of anything at a truly biological level (e.g., health status, fitness, or fecundity) because it is easily customized, and, in addition to clothing, hair is the feature that we most readily change temporarily to express ourselves (1). All of this is an important part of our psychology, especially of physical attractiveness (2,3). Curliness is not only an important component of hair style (4), it also has implications for technical performance, especially for people with very curly-textured hair, because of an increased tendency to catch and tangle (5–7). The fur coats of most mammals also rely on some hairs being curly to fill space and trap air for insulation (8,9). In domestic animals, such as sheep and angora goats, hair curliness (related to properties called crimp and bulk) has implications for the uses and value of their wool and the survivability of livestock in different environments (10). As a biomimetic model for protein-based shape memory materials, curly and straight hair could play a key role in informing the J. Cosmet. Sci., 72, 643–654 (November/December 2021)

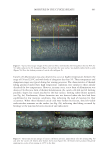
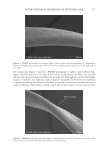
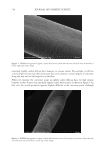
644 JOURNAL OF COSMETIC SCIENCE development of new bio-based materials composed of keratin and other similar fibrous biomolecular assemblages (11,12). WHAT IS CURL? Curliness can be intrinsic or induced. Here our focus is on intrinsic curliness. Intrinsic curliness is the shape built into a hair shaft during its growth in the follicle, and it is this shape to which an untreated hair returns when relaxed in water and dried without mechanical constraint (13). Imposed curvature is any chemically or physically induced change to intrinsic curvature, for example, from drying a fiber in a constrained state, heating a fiber in a constrained state, or inducing disulfide exchange via a permanent set technology (4). For an individual’s hair, the intrinsic curliness is what induced changes must build upon, and it is this intrinsic scenario that we still do not fully understand. What shape is curliness? For a single hair shaft, curl is three-dimensional and varies along its length. Curl is therefore a coil, something like a spring, at any one point along its length. Describing three-dimensional curliness mathematically requires each point along a hair to be described in terms of curvature and torsion (14) (Figure 1A). Measuring unconstrained hairs in three dimensions is time intensive and expensive (Figure 1B). However, constraining fibers into two dimensions and measuring only curvature is quick and relatively inexpensive. Constrained curvature data have proven to be relatively comparable to the extent that the Figure 1. Measuring curliness. (A) Curvature and torsion are three-dimensional components of hair curl. Curvature is measured on a plane that is defined by three points. Here curvature is measured on the infinite plane defined by points 1, 2, and 3, and the plane defined by points 2, 3, and 4. Torsion at midpoint between 2 and 3 is the angle between the two infinite planes (1, 2, 3 and 2, 3, 4) divided by the distance between 2 and 3. Some examples, of varied curvature and torsion. (B) Example of a photogrammetric approach to three- dimensional hair shape using photogrammetry. (C) Example of a radial ruler against which constrained hairs are placed to measure curvature quickly.