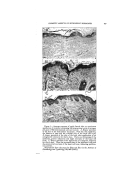
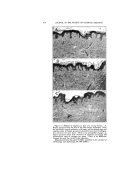
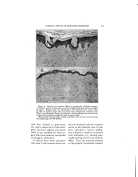
390 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS tassium oleate is known, and so is that occupied by an alcohol mole- cule. Further, the area of the cross- section of a soap molecule can be derived from the side spacing of 4.8 A. found in the liquid crystal. As a result of these two lines of evi- dence, the most probable area of a bimolecular complex in the oil- water interface is about 70 A.•' Ac- cepting this as the area per oleate residue, the total area of the inter- face can be calculated, and since the total volume of the disperse phase is known, the radius of the supposed droplets can be found. Assuming that all the oleic acid is in the inter- face, the radius of a water droplet in oil is given by the formula where //w = volume of water, and cr = total interfacial area of the droplets and is given by o' = •o where •V0 = 6 X 102a, w = weight of oleic acid, s = 70 A.•' and M = mol. wt. of oleic acid. The over- all radius of the droplet is r q- 25 A. as the oleic acid molecule is about 25 A. long. The dimensions of oil droplets in water can be calculated in a similar way, but the method is slightly more complicated. Calcu- lations were also made assuming short cylinders and lamellae for the droplets. When this was done, re- sults could be compared with ex- perimental data obtained by the two following methods. X-R^¾ S, uD•.s (19) The solutions were subjected to examination in an x-ray camera designed to study low-angle scatter- ing. Because the ratio of disperse to continuous phase was nearly 1.0, the spheres were expected to be arranged, almost in contact, on a three-dimensional hexagonal lat- tice. One would expect therefore, low-angle scattering from adjacent planes, and these Bragg spacings when corrected by multiplying by the Ehrenfest-Prins factor for liq- uids (1.23) would give the distance between the centers of adjacent droplets. Diffraction bands of this type were in fact found. They were diffuse, corresponding to liquid- type scattering, and after allowance had been made for the gap between spheres the resulting diameters were in good agreement with those cal- culated. By suitably adjusting the oil-water ratio, it was possible to bring the spheres almost into con- tact, and then the spacings were very nearly equal to the diameters of the droplets. Bands of this type were obtained with both oil- and water-continuous dispersions. In nearly all the oil- continuous systems, agreement was better with the spherical model than with either lameIlar or cylin- drical micelles. However, the case of the water-continuous systems containing comparatively large quantities of oleic acid is not so clear, and it may be that a cylin- drical model is better for them. It is obvious that the gels, which

PENETRATION AND COMPLEX-FORMATION IN MONOLAYERS 391 show streaming birefringence, can- not be treated as aggregates of spheres• but must contain cylin- drical or lamellar aggregates which are long compared to their other dimensions. As would be expected, they give sharper bands, and the spacings are nearer to those ex- pected for lamellae. Examination of them is still in progress. LmHT-Sca•r•.R•m STvm•.s (20) In order to obtain more direct evidence of the existence of mi- celiar aggregates in the dispersions, investiga- tions were carried out by a light-scattering method, using Rayleigh's formula to determine the droplet size. This is I0 - 2r=X 4 k,m•i--•2/ for right-angle scattering of a beam of unpolarized light of intensity I0 and wave-length X in the solu- tion, in which there are N particles 0f volume F and refractive index m relative to the solute, per cc., and the distance from the scattering solution to the observer is r. In these experiments, N/x was known, being the total volume of the disperse phase, and so // and hence the radius of the droplets, assumed spherical, could be calculated. When the formula was applied to systems prepared as described, it was found that the diameters cal- culated were far too small, values of 10-20 A. being indicated. This is easily explained, as Rayleigh's formula assumes that the total scat- tering is the sum of the scattering from the individual units. This is true for a gas, but is manifestly false when the scattering units are sepa- rated by less than their diameter, as we have here. Alternatively, if we regard scattering as due to con- centration fluctuations in neighbor- ing volume elements (Einstein, Smoluchowski, Debye) it is clear that fluctuations are hindered in o o•1 o-z 03 C4 NV Figure 5. highly concentrated solutions, as has indeed been shown for tobacco mo- saic virus and sucrose solutions. In order to overcome this diflSculty, series of solutions containing the same volume of disperse phase in increasing volumes of the oil (ben- zene) were examined. In all cases the intensity of the scattered light increased as the solutions were di- luted. The apparent droplet diam- eter was calculated in each case, and it was found that the log d-con-