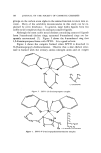
WHITE NACREOUS PIGMENTS 79 mica in another particle, and each particle behaves optically like two in- dependent TiO2 platelets. For TiOs-coated mica in a nitrocellulose (NC) coating, the reflecting unit is a thin TisO film with NC on one side and mica on the other. A general model for a thin film between two different media is shown in the diagram in Fig. 2. In the example just given, n0 would be the re- fractive index of NC, n• the refractive index of the TiO2 film, and ns that of the mica substrate. The refractive index n• of the interference film times its geometrical thickness, t, is its optical thickness n•t. The model also serves for a simple pearl essence platelet embedded in nitrocellulose, in which case no and ns have the same value, and for an interference film deposited on a glass slide. The reflections 1 and 2 from the interfaces I and II, respectively, are specular. n• Fdm Substrate Figure 2. Reflection of light by thin film. n, refractive index t, thickness Interference phenomena arise from interaction between these two re- flections. When they are exactly in phase for a given wavelength of light, they reinforce one another. When they are out of phase by half a wave- length, they are eliminated from the reflection. The reinforcement of certain wavelengths and elimination of others produce interference color. For perpendicular incidence on a thin film, the reflectance Rx for a given wavelength X is determined by a form of the general Fresnel for- mulas for reflection of light (2): cos (nx -- nO'•2(n• -- n•'• 2 _ 2[/n• -- no'•(n• -- n•) 4rn•t l+ + no/ + x,n + no/Xn + cos-- All the terms in parentheses are positive when the refractive index of the film is higher than that of the medium on either side, i.e., n• 2 no and n• n2, which is the situation now under discussion. The equation con- siders the effect of the phase difference on reflectance at a given wave- length. The total phase difference consists of two contributions: (a) the

80 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS phase difference 4•rnlt/X arising from the optical thickness nit of the film, and (b) the phase change of half a wavelength which occurs when light traveling in a medium of lower refractive index is reflected at the surface of a medium of higher refractive index, as is the case with reflection 1. The equation also takes into account the effect of the relative magnitudes of the refractive indices of the film and the adjacent media. An interesting characteristic of optical thickness is that it is not con- stant for a given film even though the geometrical thickness, t, of the film is obviously constant, since nl usually varies with wavelength. Refractive index in that case is higher at low wavelength (except for different be- havior in the proximity of absorption bands). The size of this effect, i.e., the optical dispersion, depends on the substance of which the film is com- posed. Interference also occurs with films too thin to produce interference colors, i.e., films less than about 190 nm in optical thickness. Equation 1 was used to calculate reflectance from very thin single films of anatase TiO2 on glass. For this example, no is 1.00 for air, n2 is 1.50 for glass, and nl varies from 2.86 at 400 nm to 2.49 at 700 nm for anatase, using the average of the refractive indices for the ordinary and extraordinary rays. Reflectance curves for anatase films of optical thickness 0 to 170 nm are shown in Fig. 3. Optical dispersion was taken into account however, the stated optical thicknesses are based on the refractive index 2.54 for the sodium D line (589 nm). The reflectance for optical thickness 0 is sim- ply that of the glass substrate. Reflectance in the visible range increases with optical thickness, as seen by the successively higher levels of the curves for 10, 20, 40, 60, 80, and 100 nm. The reflectance at the blue end of the spectrum is greater than that at the yellow thus, the reflection color for these curves is blue-white. The film for optical thickness 100 nm has a maximum reflectance at about 46% near 400 nm. Further increases in thickness produce a series of reflection curves of changing shape. The curve for 110 nm has a maxi- mum at 415 nm. The maximum for films of increasing thickness shifts to longer wavelength. The reflection color therefore changes from bluish white at 100 nm through yellowish white at 150 nm to whitish yellow at 170 nm. Maximum reflectance falls to about 40% as the wavelength of the maximum increases, a consequence of optical dispersion. These curves express both the color and magnitude of the reflection. The familiar simple interference equations describe the positions of max- ima and minima without providing magnitudes. These simple equations