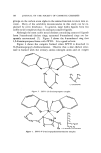
WHITE NACKEOUS PIGMENTS 81 45- 40- 55- 50- 25- 20- 15- I0- •o ,½oo ,½.•o 5bo 53o 6bo c•o •o0 Wovelenqth (rim) Figure 3. Calculated reflectance curves for single TiO.films of various optical thicknesses on glass may be derived from equation 1 by differentiating Rx with respect to x and setting dRx/dx: O. These expressions are ntt= (2m-- 1)X ... /4 (2) for the position of a reflection maximum, and n½ = 1)Xm,/2 (3) for the position of a reflection minimum. In these equations rn is a small integer, e.g., 1, 2, 3, etc., which provides for the fact that given values of kmax and Xmin recur at different film thicknesses because of the cyclical na- ture of the interference effect. For the white films under consideration here, m is 1. Equations 2 and $ are for the special case of normal inci- dence on a film which is adjacent to media of low refractive index on either side. Equation 2 applies to those curves of Fig. 3 which have definite max- ima. (Figure 3 shows only the visible part of the spectrum. Some of the thinner films which do not have a maximum in Fig. 3 have maxima in the

82 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS near ultraviolet.) Let us consider the application of equation 2 to the 140-nm curve. It has a maximum at about 530 nm. Substituting this value for Xmax and taking rn as 1, the calculated optical thickness is 530/4 or 133 nm. The solution is not ex,actly 140 nm because the 140-nm label in Fig. 3 is based on the refractive index of anatase at 589 nm rather than at 530 nm. A moment's consideration reveals the relationship between the re- flection maximum and the phase difference. A reflection maximum oc- curs,according to equation 2 when the optical thickness equals x/4. Re- flection 2 passes through the film two times and thus travels 2x/4 or half a wavelength farther than reflection 1. As was mentioned above, a phase change of half a wavelength takes place in reflection 1 at the low/high in- dex interface. Adding these two half-wavelength phase differences to- gether gives a phase difference of a whole wavelength, which means that reflection 1 and reflection 2 are exactly in phase and therefore produce a reflection m•imum. There are no reflection minima in the curves of Fig. 3 except for the 0-nm curve which is entirely "minimum." The origin of this curve may be seen in equation 3. When m is 1, the use of any value whatsoever for Xm•, gives a value of 0 for optical thickness. Thus, all wavelengths are at a minimum for optical thickness 0. If n0 and n2had been equal in the model used to calculate Fig. 3, Rx for n•t • 0 would have been 0 through- out instead of 4%. An experimental example of this case is seen when the liquid in a soap film drains out until only two monomolecular films are left: the resulting "black film" reflects no light. The value o• the reflectance at a maximum in the reflectance curve can be derived from equation 1 by substituting Xinax/4 for nit. Equation 1 may then be simplified to [n• -- non•] • Rm• = • + nons/ (4) which, for the special case when n0 and n2 are the same, becomes These equations show how •eatly reflectance depends on the differ- ence between the refractive indices of the film and the surrounding me- dia. If there were no difference in refractive index, reflectance would be 0. The greater the difference, the greater the reflect•ce.