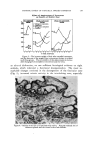
SCALE-UP CONSIDERATIONS IN COSMETIC MANUFACTURE 261 ri-t----,_•i•, r• Iz-- -•-'.•.,:r .... -i-' : F,,F-W-, C• !:11 '--[-l, TIq•,r .... /- •-['.'Fr ! ,•-••,--:T :-'r • .... t'l-rr? ,., ' --'hOE'-TURB•N E- BA FF LED •',1 / • I•!•"• I . *!!Ill' I I I!1•'!. : , : I,,, ,' , , I-FFi ' I • , i I i ! I , ,•,,' I I I !i',!' i:i•- 5---½_-•2 i_ •. .6_-•-_--_•=t• e::_ _•_ ._• '"'•A FFL ED-OR- •FF CENTER ß ": ! !•'il.11 ' :' 'H• Ill,l:. •-:.'--' -r--'--l-?, i ---'.'---•- '[41" ----t- '?.:,rl- '' ' :i : I I '1 • 5 • • 5 I0 $ 10 4 I0 5 10 6 D IMPELLER DIAMETER N IMPELLER ROTATIONAL SPEED •' LIQUID DENSITY JJ. LIQUID VISCOSITY P POWER g GRAVITY CONSTANT Figure 3.-•Power number Reynolds number curve for several impeller types. and surface tension force. A measurement of the fluid movement in the tank then can be given by the applied force to the sum of each individual resisting fluid force. Since viscosity is often a major force, the ratio of applied force to viscous force gives a group that is commonly used in many mixing scale-up correlations. This is the Reynolds number and is an important characteristic of many mixing operations. Power Drawn by an Impeller At this point, it is important to define the difference between the power drawn by an impeller at a given diameter and speed, and the speed and di- ameter required to carry out the mixing process. Correlations have been developed to relate the power drawn by a mixing impeller to the speed and diameter of the impeller as well as its shape, tank shape and fluid proper- ties. These correlations use dimensionless groups--the Power number and the Reynolds number. Th•s curve is shown in Fig. 3 for several typical impeller types. This allows us to predict the horsepower to be drawn by an impeller in a given mixing situation. It holds for geometrically similar systems of any size, all the way from small laboratory equipment up to large plant size. Take the fiat blade turbine impeller as an example. In low viscosi- ties, the Reynolds number is high and under these conditions the power drawn by an impeller is proportional to the specific gravity of the liquid and the cube of the impeller speed and the fifth power of the impeller di- ameter.

262 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS P = o NaD • In the viscous range, in which the Reynolds numbers are low, the curve has a slope of -1, which indicates that the power varies directly with vis- cosity, the square of the impeller speed and the third power of the diameter, P = I• N2D a Between these areas is a transition area where intermediate exponents apply. Once the impeller type to be used has been chosen, we have only two possible choices of the three variables, power, speed and diameter. We must choose any two of these variables to define the process job the mixer will do, then compute the third variable from the curve in Fig. 3. It is again emphasized that the curve shown in Fig. 3 does not tell us any- thing about the process job the mixer is doing. The usual method is to choose the power and impeller diameter to do the process job and then compute the impeller speed. The choice of what power and diameter to use in the process .job is the main topic of our dis- cussion here on scale-up. VISCOSITY One of the fluid properties influencing the selection of a mixer is the viscosity of the fluid. Table 1 shows the five most common classifications of fluid viscosity. Fluid viscosity is defined as the ratio of shear stress to shear rate. For example, if we apply a given shear stress to the fluid, either by a rotating impeller in a viscosimeter or a rotating mixing impeller, then the velocity pattern, or shear rate, will be determined by the viscosity of the fluid. TABLE 1.--RHEoLOGY DEFINITIONS Definition ß Effect on Viscosity,/•, of- Time Increase Shear Rate Increase Newtonian No effect No effect Non-Newtonian Pseudo-plastic No effect Decrease Dilatant No effect Increase Thixotropic Decrease No effect Rheopectic Increase No effect If at a wide variety of shear rates and shear stresses, the viscosity is constant, then we have what is called a NewtonJan fluid. If, on the other hand, at a given shear rate and shear stress, the viscosity is one value and at another rate has another value, then we have what is termed non- Newtonian behavior. Or, if the viscosity changes with time, we have non- NewtonJan behavior. If the relationship between shear rate and shear stress is as shown on Fig. 4, then we have the definitions listed. In addition, if' at a given shear