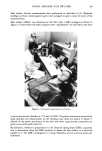
236 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS 6, Points A to B). The weights were then removed from the fibers and an "initial elastic recovery" (IER) (Figure 6, Points B to C) observed, followed by a period of creep recovery (Figure 6, Points C to D), and then creep once again (Figure 6, Points D to E) when the experiment was terminated at 44.6 hours. The "initial elastic deflection" was studied in detail, and the fiber behavior in this region is found to approximate spiral spring theory. Several years ago, on the basis of torsional measurements, Bogaty (9) suggested that the performance of hair coils is analogous to engineering spring theory. Spiral spring theory predicts that ideal coil springs deflect under load in a manner described by the equation depicted in Figure 7 CPD3N F= Gd 4 F = DEFLECTION OR EXTENSION OF SPRING I i N: No. OF SPIRALS i G = MODULUS OF RIGIDITY C: CONSTANT I d: DIAMETER OF HAIR (WIRE) P = LOAD OR FORCE I D = DIAMETER OF SPIRAL I Figure 7. Schematic of spiral spring and formula for round wire springs. (10). This equation predicts that the deflection of a hair fiber, under small loads and deflections, is inversely proportional to the 4th power of the spring diameter (hair fiber diameter), and proportional to the 3rd power of the spiral (coil) diameter. Both of these relationships were explored. Table V summarizes the data comparing the initial deflection with hair fiber diameter, which actually is governed by fiber stiffness and torsional resistance, because the test is with single fibers. Testing mathematically for the best empirical fit for these data shows that 84 percent of the variation in elastic deflection can be explained by the fourth power of the fiber diameter, and this relationship is highly significant (F calc. = 109 F required = 4.45). However, a somewhat better fit is provided by the 3rd and 2nd power relationships. This demonstrates that spiral spring theory can serve as a general guide for predicting

LOAD-ELONGATION OF HAIR COILS 237 Table V Initial Deflection and Fiber Diameter F = KP/d r 2 d d 2 d • d 4 F = Elastic deflection K = Constant P = Load on spring d = fiber diameter r 2 = index of determination 0.78 0.90 0.91 O.84 certain aspects of hair fiber behavior, but since hair fiber curls are not ideal round elastic springs, one must not expect a perfect fit to coil spring theory. Another test of spiral spring theory relates to the diameter of the coil or spiral. Here hair fibers 30 cm long were water set on rods 7.98 mm diameter. Then a small weight was added, and the deflection measured immediately. These same fibers were water set once again on 19 mm diameter rods and then on 32 mm diameter rods, once again recording these same measurements. The data from this experiment are summarized in Table VI. Table VI Effect of Coil Diameter Relative Ratio D N D 3- N D 3 ß N Deflection 9.5 11 9,431 1.00 1.00' 19.9 4.5 35,463 3.76 3.34 30.6 2.9 83,093 8.81 6.68 D = Diameter of coil (ram) N = # of spirals or coils *0.88 cm with 0.802 mg weight (mean response from 5 different fibers of varying diameter). These data show a significant relationship beyond the ce = 0.01 level for the calculated and found values, i.e., as one increases the size of the coil there is approximately a third power response between the coil diameter and the deflection or uncoiling that results by adding weight to a hair fiber coil. This result is similar to the diameter experiment, and confirms the utility of coil spring theory for predicting short term hair fiber behavior under light load at low constant relative humidity. The data summarized in Table VII illustrate further the effects of load on single hair fiber coils as depicted in Figure 6, and represent results from 19 hair fibers of varying diameter (50 to 99 microns) and added weights (0.182 to 2.26 rag). The weight selected for each fiber was via random numbers (for details see Elastic and Creep Behavior Measurements of Experimental section). The data expressed in Table VII are from multiple linear regression equations considering change in fiber length as dependent variable, and fiber diameter and added weight as independent variables. With regard to elastic deflection, the data show a good fit with 89 percent of the variation in fiber deflection explained by fiber diameter (lst power) and added weight