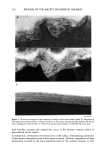
HAIR DAMAGE 191 Hair-S2 -1 I • • i • • • 0 200 400 600 TIME (sec) Figure 8. Wetting force curve of a physically rubbed human hair fiber in water. of this sample fluctuated highly, showing that the surface damage along the fiber axis was very inhomogeneous after the rubbing treatment. These results, obtained for heavily damaged hair samples, show that the wetting force increases not only upon chemical treatment but also upon physical treatment. We are currently evaluating weakly dam- aged hair fibers. In Table III, the advancing and receding contact angle data of untreated and damaged hair fibers are summarized. Averaged values of 0 for hair fiber samples decrease upon chlorination, and also correlate with the degree of chlorination however, the fluctuation in data among the samples is very high, as shown by the standard deviation values. These results strongly support the validity of our method using an electrical capacitance technique. The results shown here are consistent with the prediction by the equation of Washburn (11), which shows that the rate of water transport is influenced by the advancing contact angle values, if the radius of the capillary is constant. Table III Advancing and Receding Wettabilities of Variously Treated Human Hair Fibers a Advancing Receding Sample cos 0 a 0 a (deg) cos O• O• (deg) Untreated -0.21 102 -+ 5.4 0.57 55 +- 3.6 Chlorinated DCCA 3% b 0.37 68 +- 15.3 0.97 12 +- 12.0 DCCA 6% b 0.57 54 +- 10.9 0.95 11 -+ 10.3 DCCA 10% • 0.66 48 +- 9.7 1.13 0 Rubbed c 0.08 85 +- 10.3 0.95 18 + 10.1 a Each value is averaged for 15 fiber samples, and the standard deviation values are also shown for 0• and 0•. u Dichloroisocyanuric acid. c Rubbed against CC-1500 sandpaper.

192 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS CONCLUSION The degree of damage of hair fibers was determined using an electrical capacitance technique, and the results were compared with those obtained using the Wilhelmy principle. The water transport behavior along a hair fiber bundle is strongly influenced by the damage. In addition, the degree of influence depends on the degree of damage to the hair fibers. Therefore, the method of water transport measurement along a hair fiber bundle using an electrical capacitance technique is useful and convenient in eval- uating the degree of damage to hair fibers. ACKNOWLEDGMENTS This work was partially supported by the Ministry of Education, Japan, Grant No. 04558019, for which we are grateful. H.I. acknowledges Heian Jogakuin for the grant (Tokubetsu Kenkyuhi). REFERENCES (1) J. H. Bradbury, "The Structure and Chemistry of Keratin Fibers," in Advances in Protein Chemistry (Academic Press, New York and London, 1973), pp. 111-211. (2) D.J. Evans, J. D. Leeder, J. A. Rippon, and D. E. Rivett, Separation and analysis of the surface lipids of the wool fiber, Proc. 7th Int. Wool Textile Res. Conf, (Tokyo), vol. 1, 135-142 (1985). (3) H. Ito, and Y. Muraoka, Water transport along textile fibers as measured by an electrical capacitance technique, Textile Res. J., 63, 414-420 (1993). (4) J. Wilhelmy, Ober die Abhi/ngigkeit der Capillariti/ts-Constanten des Alkohols von Substanz und Gestalt des benetzten festen KiSrpers, Ann. Physik, 119, 177-217 (1863). (5) B. Miller and R. A. Young, Methodology for studying the wettability of filaments, Textile Res. J., 45, 359-365 (1975). (6) K. R. Makinson, "Practical Methods of Shrinkproofing", in Shrinkproofing of Wool (Marcel Dekker, New York, 1979), pp. 295-326. (7) H. Ito, H. Sakabe, T. Miyamoto, and H. Inagaki, Fibrillation of cortex of Merino wool fibers by freezing-thawing treatment, Textile Res. J., 54, 397-402 (1984). (8) L. S. Penn and B. Miller, Advancing, receding, and "equilibrium" contact angles, J. Colloid Interface Sci., 77, 574-576 (1980). (9) Y. K. Kamath, C. J. Dansizer, and H.-D. Weigman, Wetting behavior of human hair fibers, J. Appl. Polym. Sci., 22, 2295-2306. (10) Y.-L. Hsieh, M. Wu, and D. Andres, Wetting characteristics of poly (p-phenylene terephthalamide) single fibers and their adhesion to epoxy, J. Colloid Interface Sci., 144, 127-144 (1991). (11) Washburn, E. W., The dynamics of capillary flow, Phys. Rev., 17, 273-283 (1921).