686 JOURNAL OF COSMETIC SCIENCE (19) W. Voigt, Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper, Ann. Phys., 274(12), 573–587 (1889). (20) A. Reuss, Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech., 9(1), 49–58 (1929). (21) C. Popescu and F.-J. Wortmann, HPDSC evaluation of cosmetic treated human hair, Rev. Roum. Chim., 48(12), 981–986 (2003). (22) C. Popescu and C. Gummer, DSC of human hair: a tool for claim support or incorrect data analysis? Int. J. Cosmet. Sci., 38(5), 433–439 (2016). (23) F.-J. Wortmann, G. Wortmann, and C. Popescu, Linear and nonlinear relations between DSC parameters and elastic moduli for chemically and thermally treated human hair, J. Therm. Anal. Calorim., 140, 2171–2178 (2020). (24) A. R. Haly and J. W. Snaith, Differential thermal analysis of wool–the phase-transition endotherm under various conditions, Text. Res. J., 37(10), 898–907 (1967). (25) J. Cao and F. Leroy, Depression of the melting temperature by moisture for alpha-form crystallites in human hair keratin, Biopolymers, 77(1), 38–43 (2005). (26) M. L. Williams, R. F. Landel, and J. D. Ferry, The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids, J. Am. Chem. Soc., 77(14), 3701–3707 (1955). (27) C. Popescu and F.-J. Wortmann, The Behaviour of Keratins at High Temperature, Krakow, Poland, 27–31 Aug 2006, 9th European Symposium on Thermal Analysis and Calorimetry: Polish Society of Thermal Analysis and Calorimetry. (28) W. G. Crewther, The stress–strain characteristics of animal fibers after reduction and alkylation, Text. Res. J., 35(10), 867–877 (1965). (29) W. G. Crewther, The effects of disaggregating agents on the stress–strain relationship for wool fibers, Text. Res. J., 42(2), 77–85 (1972). (30) B. M. Chapman, A mechanical model for wool and other keratin fibers, Text. Res. J., 39(12), 1102–1109 (1969). (31) M. Baias, D. E. Demco, C. Popescu, R. Fechete, C. Melian, B. Blümich, and M. Möller, Thermal denaturation of hydrated wool keratin by 1 H solid-state NMR, J. Phys. Chem. B, 113(7), 2184–2192 (2009). (32) D. Istrate, C. Popescu, M. Er Rafik, and M. Möller, The effect of pH on the thermal stability of fibrous hard alpha-keratins, Polym. Degrad. Stab., 98(2), 542–549 (2013). (33) D. Istrate, C. Popescu, and M. Möller, Nonisothermal kinetics of hard α-keratin thermal denaturation, Macromol. Biosci., 9(8), 805–812 (2009). (34) M. Baias, D. E. Demco, D. Istrate, C. Popescu, B. Blümich, and M. Möller, Morphology and molecular mobility of fibrous hard α-keratins by 1 H, 13 C, and 129 Xe NMR, J. Phys. Chem. B, 113(35), 12136–12147 (2009). (35) M. Kadir, X. Wang, B. Zhu, J. Liu, D. Harland, and C. Popescu, The structure of the “amorphous” matrix of keratins, J. Struct. Biol., 198(2), 116–123 (2017). (36) M. Feughelman, A model for the mechanical properties of the α-keratin cortex, Text. Res. J., 64(4), 236–239 (1994). (37) J. W. S. Hearle, A critical review of the structural mechanics of wool and hair fibres, Int. J. Biol. Macromol., 27(2), 123–138 (2000). (38) M. Kadir, Phonon and Spin Diffusion in Single Hair Fiber: Structure of the Amorphous Matrix of Keratins, Redbank, New Jersey, June 8–9 2016, 7th International Conference on Applied Hair Science: TRI Princeton. (39) D. Harland, Hair’s multi-scalar architecture, Redbank, New Jersey, June 8–9 2016, 7th International Conference on Applied Hair Science: TRI Princeton.

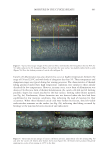
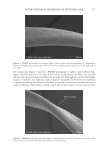
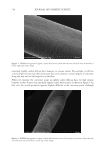
687 Address all correspondence to Manuel Gamez-Garcia, mgamez-garcia@ashland.com Moisture in the Cuticle Sheath: Effects on Hair Mechanical and Cosmetic Properties MANUEL GAMEZ-GARCIA Ashland Specialty Ingredients, Bridgewater, New Jersey, USA (M.G-G.) Synopsis The role of moisture in the cuticle sheath has not been properly explored so far. In this paper, analysis and experiments indicate that moisture variations in the cuticle sheath have a significant impact on its shear and tensile modulus and, therefore, on the overall hair mechanical and cosmetic properties. Analysis shows that if there is an imbalance in the required moisture content in the cuticle cell inter- and intralayers, steep layer moduli mismatches and stress concentrations are generated across interfaces. Imbalances of this type often arise when the hair has very low levels of moisture or when it is transiently subjected to high temperatures, becoming more severe with tensile extensions. For instance, at high elongations and near the yield point, the intermediate filaments in the cortex undergo an alpha to beta transformation. This keratin phase transition occurs at both low- and high-moisture conditions and causes the cortex tensile modulus to decrease, allowing for higher deformations without severe stress buildup. In contrast, at high elongations, the cuticle sheath has no such stress dissipation mechanism, and high-stress concentrations appear across the cuticle cells. Therefore, moisture loss in the cuticle cells accompanied by extensions aggravate stress concentrations resulting in damage at the cuticle cell cement boundaries. INTRODUCTION When studying the physical and cosmetic behavior of hair, more effort should be placed on analyzing both cortex and cuticle sheath properties. Unfortunately, too often, more attention is given to the properties of the cortex, and those of the cuticle sheath are ignored. Such a biased approach can lead to the wrong conclusions. A typical example of this can be found in studies on hair moisturization. Very often, we tend to consider that the effects of moisture on the overall hair cosmetic properties depend solely on the moisture content of the cortex. In doing so, we neglect the role that moisture in the cuticle sheath may play in this endeavor. Incidentally, it should be mentioned that recently, the hair cosmetic community has started to realize that moisture in the cortex may have little or no correlation at all with the sensorial and subjective properties of moisturized hair (1). It is quite possible that the sensorial properties associated to hair moisturization depend less on the cortex moisture and more on the effects of moisture in the cuticle sheath. This is because of the cuticle sheath’s position at the hair surface. At this point, it is difficult to make a definitive assertion in this direction until more data and research elucidate this question. We can be certain that, in the future, studies in this direction will include J. Cosmet. Sci., 72, 687–696 (November/December 2021)