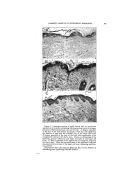
!'ii•iii!•..:Which then breaks up and forms a •:.•"i!:,'. .'•spherical shell in order to enclose )•'•i: ia given volume of water or oil in a •iii:!:iSurface of minimum area (13, 19). :.,? :: ß: •'.• .: :. : PENETRATION AND COMPLEX-FORMATION IN MONOLAYERS 389 the soap alcohol molecules, several hundred Angstrom units in diameter separated by the continuous phase. Confirmation of the postulated WATER SWOLLEN CRYSTALLIT E OIL AND WATER SWOLLEN wATER SWOLLEN LAMELLAR MICELLE MIXED CRYSTALLITE LAMELLAR MICELLE WATER WATER HYDROPHILIC OLEOM ICELLE SPHERICAL IMfC. ELLES WA' SOAP ALCOHO OLEO•HILIC HYDROMICEM. E Figure 4.--The phenomena of sofubilization of soap crystal lamellae by non-polar oils and penetration of the monolayer lattice by polar oils in the formation of micelies and emul- SLOBS. Thus, Schulman and Hoar (18) sug- gested that these transparent, fluid dispersions consisted of droplets, sur- rounded by a mixed monolayer of structure of the fluid dispersions was sought in three ways. In the first place, the area occupied at the air- water interface by a molecule of po-

390 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS tassium oleate is known, and so is that occupied by an alcohol mole- cule. Further, the area of the cross- section of a soap molecule can be derived from the side spacing of 4.8 A. found in the liquid crystal. As a result of these two lines of evi- dence, the most probable area of a bimolecular complex in the oil- water interface is about 70 A.•' Ac- cepting this as the area per oleate residue, the total area of the inter- face can be calculated, and since the total volume of the disperse phase is known, the radius of the supposed droplets can be found. Assuming that all the oleic acid is in the inter- face, the radius of a water droplet in oil is given by the formula where //w = volume of water, and cr = total interfacial area of the droplets and is given by o' = •o where •V0 = 6 X 102a, w = weight of oleic acid, s = 70 A.•' and M = mol. wt. of oleic acid. The over- all radius of the droplet is r q- 25 A. as the oleic acid molecule is about 25 A. long. The dimensions of oil droplets in water can be calculated in a similar way, but the method is slightly more complicated. Calcu- lations were also made assuming short cylinders and lamellae for the droplets. When this was done, re- sults could be compared with ex- perimental data obtained by the two following methods. X-R^¾ S, uD•.s (19) The solutions were subjected to examination in an x-ray camera designed to study low-angle scatter- ing. Because the ratio of disperse to continuous phase was nearly 1.0, the spheres were expected to be arranged, almost in contact, on a three-dimensional hexagonal lat- tice. One would expect therefore, low-angle scattering from adjacent planes, and these Bragg spacings when corrected by multiplying by the Ehrenfest-Prins factor for liq- uids (1.23) would give the distance between the centers of adjacent droplets. Diffraction bands of this type were in fact found. They were diffuse, corresponding to liquid- type scattering, and after allowance had been made for the gap between spheres the resulting diameters were in good agreement with those cal- culated. By suitably adjusting the oil-water ratio, it was possible to bring the spheres almost into con- tact, and then the spacings were very nearly equal to the diameters of the droplets. Bands of this type were obtained with both oil- and water-continuous dispersions. In nearly all the oil- continuous systems, agreement was better with the spherical model than with either lameIlar or cylin- drical micelles. However, the case of the water-continuous systems containing comparatively large quantities of oleic acid is not so clear, and it may be that a cylin- drical model is better for them. It is obvious that the gels, which