82 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS near ultraviolet.) Let us consider the application of equation 2 to the 140-nm curve. It has a maximum at about 530 nm. Substituting this value for Xmax and taking rn as 1, the calculated optical thickness is 530/4 or 133 nm. The solution is not ex,actly 140 nm because the 140-nm label in Fig. 3 is based on the refractive index of anatase at 589 nm rather than at 530 nm. A moment's consideration reveals the relationship between the re- flection maximum and the phase difference. A reflection maximum oc- curs,according to equation 2 when the optical thickness equals x/4. Re- flection 2 passes through the film two times and thus travels 2x/4 or half a wavelength farther than reflection 1. As was mentioned above, a phase change of half a wavelength takes place in reflection 1 at the low/high in- dex interface. Adding these two half-wavelength phase differences to- gether gives a phase difference of a whole wavelength, which means that reflection 1 and reflection 2 are exactly in phase and therefore produce a reflection m•imum. There are no reflection minima in the curves of Fig. 3 except for the 0-nm curve which is entirely "minimum." The origin of this curve may be seen in equation 3. When m is 1, the use of any value whatsoever for Xm•, gives a value of 0 for optical thickness. Thus, all wavelengths are at a minimum for optical thickness 0. If n0 and n2had been equal in the model used to calculate Fig. 3, Rx for n•t • 0 would have been 0 through- out instead of 4%. An experimental example of this case is seen when the liquid in a soap film drains out until only two monomolecular films are left: the resulting "black film" reflects no light. The value o• the reflectance at a maximum in the reflectance curve can be derived from equation 1 by substituting Xinax/4 for nit. Equation 1 may then be simplified to [n• -- non•] • Rm• = • + nons/ (4) which, for the special case when n0 and n2 are the same, becomes These equations show how •eatly reflectance depends on the differ- ence between the refractive indices of the film and the surrounding me- dia. If there were no difference in refractive index, reflectance would be 0. The greater the difference, the greater the reflect•ce.

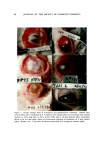
WHITE NACREOUS PIGMENTS EXPERIMENTAL The use of a recording goniospectrophotometer in measuring specular reflectance of nacreous pigment coatings has been described (3). It has been shown that specular reflectance is a measure of nacreous luster, al- though a full description ot• nacreous characteristics requires considera- tion of diffuse reflectance and transmittance as well. The present work utilized the same technique for preparation of drawdowns in nitrocellu- lose and for measuring spectrophotometric curves with the Leres Trilac spectrophotometer. • All specular reflectance curves were made with an angle of incidence of 15 ø to the normal and a viewing angle of 15 ø, i.e., at -- 15 o / 15 ø. Reflectance was measured relative to that of a pressed cake of barium sulfate. Different portions of a mica sample were coated with uniform anatase layers ot• various thicknesses (4, 5). Drawdowns in nitrocellulose lacquer were prepared at such concentrations that the mica content remained un- changed (Table I). In this way, the number of particles in the several drawdown solutions was kept constant. The estimated optical thick- nesses were calculated (see footnote to Table I) from the known compo- sitions of the pigments and the shapes of the spectrophotometric reflec- tance curves, which are shown in Fig. 4. Although a drawdown consists not of a single reflecting film but of numerous platelets throughout the depth of the nitrocellulose coating as in Fig. 1, the spectrophotometric curves of these drawdowns bear a strik- ing resemblance to the calculated curves of Fig. 3. The 0-nm film, as be- fore, is a straight line, which in this case represents the gloss of the draw- down lacquer containing uncoated mica. The thinnest film (36 nm) has the same shape as the 40-nm calculated film of Fig. 3. The 108-nm film is the first one which has a maximum in the visible range, like the 110-nm film of Fig. 3. The curves are not exactly like the calculated curves be- cause in the experimental system the ret•ractive indices no-n•-n2are 1.50- ca. 2.3-1.58 for NC/anatase/mica instead of 1.O-ca. 2.5-1.50 for the theo- retical model. The refractive index of anatase in the pigment is lower than that in the theoretical model because the deposited anatase has sub- microscopic voids which reduce the refractive index of the layer. DISCUSSION The theoretical curves are based on the interference properties of films which are thinner than those which produce interference color. * Kollmorgen Color Systems, Attleboro, Mass. 02703.