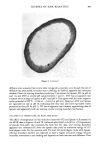
KINETICS OF HAIR REDUCTION 305 We assume that the reaction is pseudo first-order on the outside of the boundary, and that the number of bonds exposed to reduction at any time can be approximated by X(t) divided by the average thickness of the hair, T, the root mean square of the two semi-diameters (a and b)of the elliptical hair shaft (T -- •/(a 2 + b2)/2)). The number of disulfide bonds remaining uncleaved is again assumed to be proportional to the tensile stress, F. With these assumptions, the rate of stress relaxation can be approximated by: 4. dF/dt=--(kCoA/T)Ft •/2. With the initial condition that F = F(O) when t = 0 the solution of the equation is: 5. F(t) = F(O) exp(-(2/3•KC0/T)t'/•'), where the apparent rate constant K is kA. The approximations will only be good at early times when the hair can be considered to be a semi-infinite medium after the diffusion boundary reaches the center of the hair the remaining reaction should be pseudo first-order, controlled by the reaction rate constant k. For testing and using the moving boundary model for SFTK kinetics, we arbitrarily define early times as those before the level of tensile stress has fallen to one half of its initial value, i.e., F(t)/F(O) = 0.5. Note that the apparent rate constant K will have units of cm x moles -1 x sec -3/2 rather than moles -1 x sec -•. This is because the constant A is proportional to the square root of the diffusion constant in unreacted hair and has units of cm x sec -1/•' (3). Equation 5 predicts the shape of the stress vs. time curve, and the nature of the dependence of the overall rate on reactant concentration and hair diameter. The moving boundary model predicts that partial reduction will leave a sharp line of demarcation in the hair with extensive reduction outside the boundary line and little or no reduction inside. By contrast, the pseudo first-order model predicts that reduction will be uniform throughout the hair at any time. Thus our SFTK models can be tested in several ways. Figure 3 shows SFTK data for the reaction of DTT with two hairs from the same head but with quite different cross-sectional dimensions. Curves calculated from equation 5 using rate constants obtained from the linear least squares fit of ln(F(t)/F(O)) vs. t 3/2 using all values of F(t)/F(O) = 0.5 are also shown. The fitted curves can hardly be distinguished from the actual data, and the apparent rate constants obtained from the two hairs are in fair agreement. SFTK curves from three sections of the same hair treated with lipoate at three different concentrations at pH 9.0, 25øC, are shown in Figure 4, along with curves obtained by fitting the data to equation 5. As in Figure 3, the fit of the calculated curves to the data is excellent. Three sections of a different hair from the same head were subjected to SFTK testing at three different concentrations of DTT. Table I shows apparent rate constants, linear correlation coefficients (r2), and the root mean squares of the average deviations (r.m.s.d) between the calculated and actual values of F(t)/F(O) for both the DTT and lipoate (Figure 4) SFTK curves, obtained from the least squares fit of the data to

-00.4 N 00.2 0 Z o XXXXXxx, ' 000000000 '"'XXx O00 XX X 0000 I I I I I I t i me (m i Figure 3. SFTK curves from hairs of different cross-sectional dimensions fit to moving boundary model. Points are actual data. Solid lines are calculated curves. 0.15 M DTT, pH 9.0, 22øC. 1. a = 0.0067 cm, b = 0.0038 cm, K = 2.2 x 10 -6 cm M -• sec -3/2 2. a = 0.0030 cm, b = 0.0023 cm, K = 1.8 x 10 -6 cm M -• sec -V2 --00. 4 N .•1 E O Z 0.0 o • X 0 0 X • X 0 • X 0 • X 0 • X 0 0 • X X 0 • X. O0 0 • XX• O0 0 ^XXXXxv•. ' OOOOOn•_ • • •^^xX •uo xxxxxxxxxxxxx 2 I I I I I I t i me (rn i tqu•e•) Figure 4. SFTK curves for lipoate at pH 9.0, 25øC fit to moving boundary model, 1) 0.15 M thiol (000), 2) 0.3 M thiol (xxx), 3) 0.6 M thiol (000). Points are actual data. Solid lines are calculated curves.