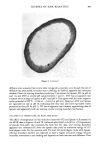
KINETICS OF HAIR REDUCTION 313 E o z I I I I I I Time (m i nu'E. ee) Figure 8. Effect of strain on SFTK curves 0. I5 M DTT, pH 9.0, 22øC. I I I I I (xd •' • (I) t51 Time (minu•es) Figure 9. SFTK curves from reactive (--) and nonreactive (---) hair, 0.6 M TG, pH 9.5, 22øC.

314 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS Individual differences in reactivity of dithiol reducing agents also occur as demon- strated by the data in Table III. The average apparent rate constants found for the six individuals studied vary over a five-fold range. These differences are probably due to biological variations in the porosity of hair rather than from chemical damage, as this Table III Individual Variations in Reactivity to Lipoate Standard Individual n K* Deviation M 10 5.1 X 10 -7 4 X 10-8 B 5 5.2 X 10 -7 6 x 10-8 C 4 7.0 X 10 -7 7 X 10-8 J 4 2.0 X 10 -6 2 X 10 -7 P 10 2.3 X 10 -6 3 X 10 -7 0.17 M Sodium Lipoate, pH 9.0, 22øC *The units on K are cm M-' sec-3/2 n = number of hairs per individual. hair was obtained from donors who claimed that they have never permed, straightened, or colored their hair. The total sulfur content and wet Young's Modulus of hair from these individuals were not found to correlate to the reactivity differences seen in Table III (8). CONCLUSIONS The work described in this communication has led us to draw the following conclusions: 1. The SFTK method is useful for basic studies of the interaction of reducing agents with hair. 2. Under some reaction conditions a moving boundary of reducing agent is formed, while under other conditions reaction occurs simultaneously throughout the hair. 3. DTT and lipoate generally react via the moving boundary mechanism, while TG kinetics are pseudo first-order at pH 9 or below, and moving boundary at pH 10 and above. 4. There are significant variations in the susceptibility of hair from different individuals to reductive treatment. While we are confident that a moving boundary is formed when indicated by SFTK curves and that the SFTK rate dependence at early times is correctly described by F(t)/F(O) = exp(--constant x t3/2), we cannot state with certainty that the exact form of the constant term is given by equation 5. The data in Figures 4 and 5 and Table I show reasonable but not exact agreement with the theory. However, equation 5 provides a convenient and fairly precise way to normalize between hairs of different dimensions or across different concentrations of reducing agents. Note that even a factor of two difference in average cross section leads to relatively little difference in SFTK curves with DTT (Figure 3). Even so, all of our concentration, pH, and temperature series were run on different sections of the same hair to minimize the possibility of artifacts due to differences in hair dimensions.