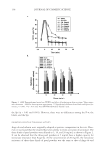
BASIC OPTICS OF EFFECT MATERIALS 87 refl ected at the interface is determined by the Fresnel equations. At normal incidence, the Fresnel equation simplifi es to equation 3: R n n n n 2 1 2 1 2 = − + [( )/( )] (3) The equation becomes more complicated for non-normal incidence. Regardless of the form, the point is the same: the larger the difference between n1 and n2, the higher the refl ection will be. For example, at the interface between media with an index of refraction of 1 (air) and 2.7 (rutile titanium dioxide), the % refl ection (at normal incidence) is 21%, while the % refl ection (at normal incidence) at the interface between media with an index of refraction of 1 (air) and 1.5 (silica) is only 4%. Light that is not refl ected at the interface enters the medium and is refracted. The refrac- tion angle θ2 is determined by Snell’s law in equation 4: n Sin n Sinθ 1 1 2 2 θ = (4) The velocity of light through a medium that is denser than space (or air) is slower than the maximum value for the speed of light. Equation 2 can be rearranged to solve for ve- locity as in equation 5: v c n = / (5) This equation means that the higher the refractive index of a medium, the slower the velocity of light through that medium. If equation 5 is substituted into equation 1, the result is equation 6: c /n = νλ (6) Since the frequency of a wave and the speed of light remain constant, the wavelength of light changes according to equation 7: λ λ 2 1 1 2 n = ( / ) n (7) Figure 2. Refl ection and refraction of incident light at the interface between media with refractive indexes of n1 and n2.

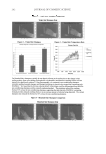
JOURNAL OF COSMETIC SCIENCE 88 INTERFERENCE OF WAVES SINE WAVE A light wave can be mathematically represented by the function in equation 8: y sin x) = ( (8) One wavelength is depicted when the function is evaluated from 0 to 2π, or 360 degrees. Figure 3 shows the sine wave. PHASE SHIFT A phase shift is the number of degrees (radians) that a wave is shifted in the x direction. The sine wave function is modifi ed, as in equation 9, where p is the phase shift: y sin x p) = − ( (9) Because 2π radians and 360 degrees represent a full circle as well as a full wavelength, there are equivalent phase shifts such that = π = π = π 0 2 (360) 4 (720) 6 (1080) π = π = π = π (180) 3 (540) 5 (900) 7 (1260) and π = π = π = π/2 /2 (90) 5 /2 (450) 9 /2 (810) 13 (1170) The result of a phase shift on the original wave is depicted in the following fi gures. Figure 4 shows a phase shift of 45 degrees, Figure 5 shows a phase shift of 90 degrees, Figure 6 shows a phase shift of 135 degrees, and Figure 7 shows a phase shift of 180 degrees. INTERFERENCE Interference occurs when two waves are in same space at the same time. When two waves interfere, the resultant wave is the sum of the y values for each x value. It is very common Figure 3. Depiction of a sine wave evaluated for one wavelength.