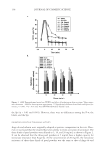
BASIC OPTICS OF EFFECT MATERIALS 99 Starting with 450 nm, fi rst determine the phase shift by taking 2π/λ × pathlength and adding π for constructive interference: ( / , / .9440 2 450 360 2 20 π π π × 1275) × + = = 20.9440 radians 1200 degrees or Next the result of interference is calculated and plotted. Table I contains the calculation and Figure 23 shows the plot for 450 nm. The amplitude of the resulting wave is the maximum magnitude, which in this example is at 150 degrees. Since the value at 150 degrees was not previously calculated, it is calculated here: Amplitude Sin(150) Sin(150 1200) 1.00 = + − = The intensity, which is the square of the amplitude, equals (1.00)2 = 1.00. Similarly, with 550 nm, fi rst determine the phase shift by taking 2π/λ × pathlength and adding π for constructive interference: ( / / .7072 2 1275) 360 2 17 1015 π π π 550 17.7072 radians or, degrees × × + = = Again, the result of interference is calculated and plotted. Table II contains the calcula- tion and Figure 24 shows the plot for 550 nm. The amplitude of the resulting wave is the Figure 23. Calculated result of interference at 450 nm. Table I Calcuation for 450 nm x y = sin(x) y = sin(x-1200) Sum 0 0 −0.86603 −0.86603 45 0.7071 −0.96593 −0.25882 90 1 −0.5 0.5 135 0.7071 0.258819 0.965926 180 0 0.866025 0.866025 225 −0.7071 0.965926 0.258819 270 −1 0.5 −0.5 315 −0.7071 −0.25882 −0.96593 360 0 −0.86603 −0.86603

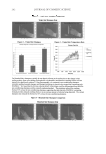
JOURNAL OF COSMETIC SCIENCE 100 maximum magnitude, which in this example is at 60 degrees. Since the value at 60 de- grees was not previously calculated, it is calculated here: Amplitude Sin(60) Sin(60 1015) 1.69 = + − = The intensity, which is the square of the amplitude, equals (1.69)2= 2.86. With 650 nm, determine the phase shift by taking 2π/λ × pathlength and adding π for constructive interference: ( / / .4663 2 650 1275) 360 2 15 π π π × × + = = 15.4663 radians or, 886 degrees Finally, the result of interference is calculated and plotted. Table III contains the calcula- tion and Figure 25 shows the plot for 650 nm. The amplitude of the resulting wave is the maximum magnitude, which in this example is at 180 degrees. Since the value at 180 degrees was previously calculated, it is read from Table III. The intensity, which is the square of the amplitude, equals (0.242)2 = 0.06. The intensities for the three primary colors are plotted to determine the total color of the interference fi lm. In addition, one can add the respective intensities for the wavelengths that correspond to constructive and destructive interference. These wavelengths were determined in the example in the section on refl ective interference. The constructive Table II Calcuation for 550 nm x y = sin(x) y = sin(x-1015) Sum 0 0 0.906308 0.906308 45 0.7071 0.939693 1.646799 90 1 0.422618 1.422618 135 0.7071 −0.34202 0.365087 180 0 −0.90631 −0.90631 225 −0.7071 −0.93969 −1.6468 270 −1 −0.42262 −1.42262 315 −0.7071 0.34202 −0.36509 360 0 0.906308 0.906308 Figure 24. Calculated result of interference at 550 nm.