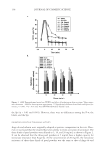
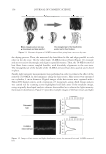
BASIC OPTICS OF EFFECT MATERIALS 93 A and W I2 is at point B. From this point, the two waves take different paths to reach point D, where interference occurs. While it is true that W I 1 travels the distance AE + ED to reach point D, W I 2 also travels the distance BD to reach point D. In the time it takes W I 2 to travel the distance BD, W I 1 travels the distance AC, which is determined by change in the wavelength in the fi lm from equation 7 so the actual pathlength difference is deter- mined by CE + ED. It turns out that the distance CE + ED can be conveniently indicated by equation 10: Pathlength difference 2dCosθ 2 = (10) The phase shift is determined by converting the pathlength difference into a fraction of the wavelength in medium n2 by multiplying by 2π/λ2, resulting in equation 11: Phase shift 4 dCosθ 2 2 = π λ / (11) Note that the wavelength is in terms of λ2, the effective wavelength while traveling in the fi lm, because the pathlength difference occurs in the fi lm. To make it more conve- nient, equation 7 can be substituted into equation 11, and assuming that n1 = 1 for air, which will be the case going forward, the result is equation 12: Phase shift 4 n dCosθ 2 2 1 = π λ / (12) Now, the phase factor can be taken out of equation 12, leaving the fi nal form of the path- length difference in equation 13: Pathlength difference 2n dCosθ 2 = 2 (13) Thus the pathlength difference and phase shift depend on the refractive index and thick- ness of the fi lm (the product of these is known as optical thickness) and the refraction angle, which is linked back to the incident angle through equation 4. REFLECTION INTERFERENCE Refl ection interference (WR) results at point D in Figure 14 when the refl ected portion of W I 2 meets the externally refracted portion of W I 1 . These two waves will constructively interfere if they are in phase. Since W I 2 refl ects off an interface where n2 n1, it has a phase shift of 180 degrees, which is equivalent to a pathlength difference of 1 /2λ. Therefore, the net pathlength difference for W I 1 must also be 1 /2λ. Thus the equation for constructive interference is in equation 14: …) 1 2 1 2 (m ) 2n dcos (m 0,1,2,3 λ = θ = 2 (14) Destructive interference of these two waves will occur if they are out of phase by 180 degrees. Again, W I 2 refl ects with a phase shift of 180 degrees, and therefore, the net path- length difference for W I 1 must be λ. Consequently the equation for destructive interfer- ence is in equation 15: …) 1 2 m 2n dcos (m 1,2,3,4 λ = θ = 2 (15)

JOURNAL OF COSMETIC SCIENCE 94 The following example demonstrates how to determine the wavelengths that in refl ection are either constructively or destructively interfered for light that is normal incident from air on a thin fi lm with a refractive index of 2.5 and a thickness of 255 nm. Solution. For normal incidence, θ2 = 0. The pathlength from equation 13 is then 2 × 2.5 × 255 × Cos(0) = 1275 nm. Use constructive interference equation 14 and plug in various values of m and solve for λ1: ( )λ ( ) ( ) 1 2 1 1 1 2 1 1 1 2 1 1 1 1275 850 2 1275 λ λ λ λ λ = = = = = = 1275 2550 nm nm 5 510 3 1275 364 1 2 1 1 nm nm ( ) .29 λ λ = = Use destructive interference equation 15 and plug in various values of m and solve for λ1: ( ) ( ) .5 ( ) 1275 1275 2 1275 637 3 1275 425 1 1 1 1 1 1 λ λ λ λ λ λ = = = = = = nm nm n nm ( ) .75 4 1275 318 1 1 λ λ = = TRANSMISSION INTERFERENCE Transmission interference (WT) also results at point D in Figure 14 when the refracted portion of W I2 meets the internally refl ected portion of W I1 . These two waves will con- structively interfere if they are in phase. Since neither wave has refl ected off an interface where n2 n1, neither wave is phase shifted. Therefore, the net pathlength difference for W I1 must be λ. Thus the equation for constructive interference is in equation 16: …) 1 2 2 m 2n dcos (m 1,2,3,4 λ = θ = (16) Destructive interference of these two waves will occur if they are out of phase by 180 degrees. Again, neither wave has a phase shift of 180 degrees therefore, the net pathlength difference for W I1 must be 1 /2λ. So then, the equation for destructive interference is in equation 17: …) 1 2 1 2 2 (m ) 2n dcos (m 0,1,2,3 λ = θ = (17) The following example demonstrates how to determine the wavelengths that in transmis- sion are either constructively or destructively interfered for light that is normal incident from air on a thin fi lm with a refractive index of 2.5 and a thickness of 255 nm. Solution. For normal incidence, θ2 = 0. The pathlength from equation 13 is then 2 × 2.5 × 255 × Cos(0) = 1275 nm. Use constructive interference equation 16 and plug in various values of m and solve for λ1: ( ) ( ) .5 ( ) 1275 1275 2 1275 637 3 1275 1 1 1 1 1 1 λ λ λ λ λ λ = = = = = = nm nm 425 n 318.75 nm ( ) 4 1275 1 1 λ λ = =