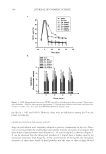
BASIC OPTICS OF EFFECT MATERIALS 101 interference is at 510 nm, with an intensity of four. The destructive interference is at 425 nm and 637.5 nm, with an intensity of zero. These values are plotted in Figure 26, where the intensities of other wavelengths were added to fi ll in the curve. COLOR TRAVEL As discussed earlier, the pathlength difference of equation 13 (and therefore the color) depends on the refractive index and thickness of the fi lm and the refraction angle, which can be tied back to incident angle. Once an effect material is made, its thick- ness and refractive index remain constant, but the incident angle can change, and therefore the color will change accordingly. Effect materials based on thin-fi lm inter- ference are said to have color travel because the color moves with changing incident angle. The degree of color travel depends on the refractive index. High-refractive- index materials have short travel and low-refractive-index materials have longer travel. When the incident angle is varied from normal incident toward a grazing angle, the pathlength gets shorter and the color travels backwards, which is opposite to the progression in Figure 22. Table IV contains a comparison of a low-refractive-index fi lm with a high-refractive-index fi lm with the same optical thickness. As the inci- dent angle is changed, the refraction angle is calculated using equation 4, followed by the pathlength. Figure 25. Calculated result of interference at 650 nm. Table III Calcuation for 650 nm x y = sin(x) y = sin(x-886) Sum 0 0 −0.24192 −0.24192 45 0.7071 −0.85717 −0.15006 90 1 −0.9703 0.029704 135 0.7071 −0.51504 0.192069 180 0 0.241922 0.241922 225 −0.7071 0.857167 0.150061 270 −1 0.970296 -0.0297 315 −0.7071 0.515038 -0.19207 360 0 −0.24192 -0.24192

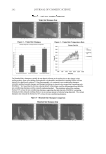
JOURNAL OF COSMETIC SCIENCE 102 Comparing the data in Table IV reveals that the refraction angle for SiO2 is greater than for TiO2 at any incident angle except for normal, where they are equal. This difference is a direct consequence to Snell’s Law of equation 4. With the optical thickness of SiO2 and TiO2 set to be equal, they have the same pathlength (and color) at normal incident. At other angles, the differences in refraction angle lead to different pathlengths (and colors). The resulting pathlengths for the low-refractive SiO2 have a larger range than for the higher-refractive TiO2, and thus the SiO2 has more color travel. The differences in color travel are better demonstrated on a color chart, as in Figure 27. While both TiO2 and SiO2 start out with the same green color, TiO2 only travels to about a blue while SiO2 travels all the way to orange. Another way to demonstrate color travel is to look at the spectral curves. Figure 28 con- tains the spectral curves for a TiO2 fi lm with the same optical thickness as in the example from the section “Color From Interference,” so that the curve at normal is the same as that in Figure 26. This curve is the one farthest to the right in Figure 28. The primary colors are highlighted. Each curve to the left is a result of a 10-degree incident angle change from the curve to the right. Note that the overall shape of the curve is not changing it is just moving to the left and the intensities of the primary colors go up and down accord- ingly, like buoys in the ocean as waves go by. Initially the curve has high intensity for green and low intensity for blue and red, resulting in a green color. As the curve shifts, Table IV Pathlength vs Incident Angle SiO2, n = 1.5, d = 250 nm TiO2, n = 2.5, d = 150 nm θ1 θ2 2nd Cos θ2 θ2 2nd Cos θ2 0 0.0 750 0.0 750 10 6.6 745 4.0 748 20 13.2 730 7.9 743 30 19.5 707 11.5 735 40 25.4 678 14.9 725 50 30.7 645 17.8 714 60 35.3 612 20.3 704 70 38.8 585 22.1 695 80 41.0 566 23.3 689 Figure 26. Resulting calculated spectral curve for 255-nm-thick interference fi lm with a refractive index of 2.5. Also shown are the intensities of the primary colors (blue, green, red) and the constructive and destruc- tive interference cases (●). The intensities of other wavelengths are used to fi ll out the curve.