304 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS Accordingly, this bias can be corrected by weighting the distribution at the surface inversely with the bubble radius (4). The final results can be expressed succinctly as rj,• = r'j-•,•-• (3) where, for the true distribution, •nr • rj,• •-• - •nr• (4) and r'j-l,k-1 is defined correspondingly for the surface. Symbol n repre- sents the number of bubbles of radius r. Thus, for example, the true ordinary arithmetic mean radius rl,0, which is defined as ,•nr/,•n for the true distribution, equals r'0,-1 which is ,•n/,•(n/r) from the surface distribution. It can also be shown that the true frequency distribution function of radii can be found from the dis- tribution function at the surface by multiplying the latter by r'o,_•/r. STABILITY Foam stability is ascribed to several factors. Before a bubble wall rup- tures, it first stretches and thins locally. This action increases the local surface area, thus momentarily decreasing the concentration of surfactant adsorbed at the surface. This decrease o.ccurs partly because the supply of surfactant within the film is limited, and partly because the surfactant requires some finite time to diffuse from the interior of the film to the surface. The resulting local increase in surface tension tends to draw the stretched (thinned) film together again, thus opposing rupture. The "healing" of the film which is based on the limited supply of sur- factant is sometimes termed the Gibbs effect, and that which is based on the diffusional lag is sometimes called the Marangoni effect. The relative importance of these two effects is still subject to dispute. With ionic surfactants the electrostatic repulsion between the parallel surfaces of the film opposes thinning and thus contributes to stability. High surface viscosity and high liquid viscosity also contribute to stability by damping the effect of local disturbances and by slowing drainage. Possible sources of disturbance include pressure fluctuation, thermal fluctuation, spontaneous vapor nucleation, ionizing radiation, external vibration, and internal stresses brought about by local changes in the bubble packing that result from the changes in bubble size caused by gas diffusion between bubbles. This last phenomenon will be discussed presently.

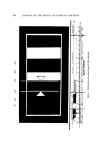
PHYSICAL ASPECTS OF FOAM 305 Activation energies of rupture, which are directly proportional to the square of the film thickness, have been derived by several workers, and critically examined (15). Fluctuations in film thickness, which produce a thinning process that grows spontaneously until rupture, have been proposed (16, 17). Once rupture begins, the hole grows very rapidly at an essentially con- stant linear velocity which, according to a simple model of momentum conservation, is equal tox/•y/tt•, where y is surface tension, t is uniform film thickness, and t• is liquid density (18, 19). The number of ruptures per unit time is thought to be kinetically of first order with respect to the number of bubbles present (20). Even in the absence of rupture, there is still another cause of foam instability and coalescence. It is the interbubble gas diffusion mentioned briefly above. This diffusion is pressure driven, and takes place from small bubbles to larger bubbles. For example, applying eq 2 to each of two spherical bubbles which are surrounded by a common liquid, and subtracting, yields eq 5, /Xpb = 2-r (• - /) (5, in which •xp, is the pressure difference between the two bubbles, r is the radius of the smaller bubble, and r' is the radius of the larger bubble. The factor of 2 appears in eq 5 because, with spherical bubbles, r = Rx __ R, and r' = The rate of gas diffusion, q, is given by eq 6, q = --JAbApo (6) where A • is the effective perpendicular area through which the gas diffuses between bubbles, and J is the permeability of the diffusion path. The resistance of this path is the sum of the resistances of the liquid layer and the two interfaces (21). The negative sign simply signifies that the gas diffuses in the direction of pressure decrease. When the liquid layer is of the order of 10 -4 cm or greater in thick- ness, its resistance is likely to control. The resistance of the two inter- faces can then generally be neglected. In such a case, eq 6 becomes e[ fectively Fick's law, q = --DA•Ap•/Ht (7) where D is the diffusivity and H is the Henry's law constant. However, the interfacial resistance should not be neglected if insoluble monolayers