306 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS are present and/or if the bubble wall is very thin, say on the order of 10 -5 cm as can occur in a very dry foam (20). As diffusion progresses, the large bubbles become progressively larger, and the small bubbles progressively smaller. In fact, some may shrink to the point of disappearance. For a small bubble surrounded by much larger bubbles, r 44 r'. Thus, 1/r' can be neglected in eq 5. By com- bining the now-simplified eq 5 with eq 6 and the ideal gas law (using atmospheric pressure, pa, in place of bubble pressure), and then integrat- ing, one obtains eq 8 for the lifetime, r, of a small shrinking bubble, r i2p a r -- 4q•JR T (8) where r• is the initial radius of the bubble, R is the gas constant, and T is the absolute temperature (4). Since all bubbles of initial radius equal to or less than ri will disappear during time •-, the total number of bubbles will decrease from (•n)0 present initially to (•n)vat time •- according to (Zn), = (2n)0 I1 - fr'F(ri)dri] (9) where F(r•) is the initial frequency distribution of bubble sizes (radii). The average bubble volume 4=ra,0a/3 at time •- can then be readily found by dividing the gas volume in the foam by (ln) , provided of course that F(r 0 is known. Combining eqs 1, 8, and 9 yields (Zn)0 (Zn)• = (1 + kay-) 3 (10) where 4RT?Jb ka - (11) Pa Experimental values for ka have been reported between 1.0 X 10 -a and 3.3 X l0 a sec -1 (20). The effect of interbubble gas diffusion on the num- ber of bubbles present can thus be estimated. The slight pressure excess within each bubble has also been used to derive an equation of state for the gas phase (as a whole) within the foam (22). Of course, the total volume of the foam also depends on the liquid content which typically drains away with time, aided by bubble coalescence due to rupture and/or interbubble gas diffusion.

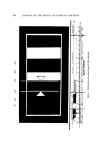
PHYSICAL ASPECTS OF FOAM 3O7 DRAINAGE After a standing column of foam has been draining for some time, the liquid content will be low at the top and high at the bottom. For many foams, the average liquid content can be approximated in terms of an exponential time decay, or in other ways. However, most of the analyses of drainage which have been offered so far require the use of empirical constants because the approaches were in large measure empirical. A more fundamental attack (11) recognizes that, at least for dry foams, the drainage takes place primarily through the Plateau borders, which essentially are randomly oriented and of curved triangular cross section (as shown in Fig. 1) with walls that are subject to a finite surface viscosity. Regular dodecahedra of equal size were taken as the model for the bub- bles. By geometry, this gives 1.952X/r 2 of PB length per unit volume of foam, where X is the volumetric fraction of gas in the foam, and r is the radius of the sphere equal in volume to a dodecahedron. From the randomness of the PB orientation, the number of PB's intercepted by a unit of cross-sectional area is half, or 0.976x/r 2 (23). The differential equation of momentum conservation for incompress- ible rectilinear steady flow was solved for a general PB, and the resulting local velocities were combined vectorially with the upward movement (if any) of the foam as a whole. The resultant velocities were then inte- grated with respect to the horizontal cross section of the vertical column to give the rate of steady drainage for a stationary foam (or the net rate of steady liquid upflow if the foam is rising). The analysis does not in- clude coalescence as such, so the results are limited to stable foams unless the extent of coalescence is available from other information. Steady drainage of a stationary foam in a column can be achieved by feeding liquid steadily to the top of the foam. For such a system, the theory relates the drainage rate to the liquid content of the foam (24). In principle, through combination with an unsteady-state mass balance over a horizontal element of differential thickness, this theory also can be applied to the unsteady drainage of a stable foam. The theory also relates the rate of foam overflow to the various in- dependent parameters by means of two dimensionless groups, oe and •. Group o is defined as 4QAgt•re/Get• or its equivalent, 41togre/lto%. Q is the volumetric rate of foam overflow on a gas-free basis (in other words, just the liquid), A is the horizontal cross-sectional area of the column, g is the acceleration of gravity, G is the volumetric rate of gas flow, t• is the dynamic liquid viscosity, uo is the superficial linear velocity of collapsed