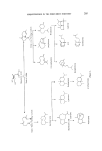
DECISION ANALYSIS 169 = oe30 000, and would be unwise to pay more than this sum for the survey. More generally, the expected value with perfect survey information is •Z {m•.ax R ii P(Zj) } . (2) The value of information is therefore given by ( Z•max Rijp(Z•)} - •ax Z R• p(Zi)} . (3) Another way of arriving at the 'value of information' is to consider the effect it has had upon the decision. If environments Zx and Z• prevail, the purchase of information has added to the costs but not to the return since decision X• would have been taken anyway. If, however Za prevails, the purchase of information prevents a loss of El00 000. Since the prior prob- ability of Za is 0.3, the information offsets an expected loss of E100 000 x 0.3 = •30 000. As already stated, on expected value grounds, provided the cost of a market survey is less than •30 000, policy three will be selected. In other words, a market survey will be carried out and policy X• or X• selected, depending upon the findings of the survey. This analysis indicates whether or not a market s•vey can be justified in a manner consistent with the manager's knowledge and judgement of the situation as expressed by his probability distribution p(Z). Imperfect information The assumption of infallibility of a market survey is, of course, not realistic. Accepting the fact that such tests are subject to error, how much is a survey worth and how would the results be used? Presumably one would not pay more for imperfect information than one would for perfect information. Here the decision-maker may or may not have a high prior feeling as to the potential of his new product. He may or may not conduct a market survey which may or may not endorse his views. This situation is best represented by a tree as follows, where a positive and negative test result represents a survey recommendation to market and not market respectively Six possible decision points can arise (A, B, C, D, E, F). First consider E. and F. Here the decision is based only on the manager's prior knowledge and would, presumably, be made in accordance with section on 'Decisions

170 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS Manager's prior opinion of the product Survey conducted ? Survey result under risk'. If a survey is undertaken, the decision point could be A or D, that is the manager's prior notion and the market test are in agreement. If this is so, the test has contributed to the cost of the decision but not, pre- sumably, to the actual return on the decision, since the same decision for points A and D will likely be made as for points E and F respectively. Consider the remaining decision points B and C. Here the survey results and manager's priors are in conflict and we still have a problem. Is the decision to be made on the basis of the manager's priors, the survey information or perhaps a mixture of both? It would appear the purchase of imperfect information is either costly and useless or leads to a situation equally imponderable with the initial decision! To confuse the issue further, at any particular stage the actual environment is unknown. In other words, even if the manager's prior feeling and the test result are in agreement, they could both be wrong! Bayes theorem gives a way out here. This is a theorem concerning probabilities and may be written (4) p(Z and X) p(z IX') =