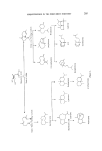
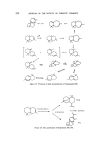
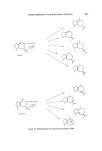
DECISION ANALYSIS 173 and the sample result X. This seems reasonable since the information X is a function of the number of people surveyed, the format of the survey, etc., whereas the manager's priors p(Z) are based upon a different source of information, namely his experience and knowledge to date. Here the broadest possible data base is used for the decision. For further reading on this topic, the reader is recommended to look at (4) and (5). SUBJECTIVE TESTS AND INFORMATION In the previous section are discussed the use of information which was essentially an objective measure of a specific quantity such as market share. We discuss in this section the value and use of tests and information which are subjective in nature. Consider the situation of, say, a soap manufacturer who wishes to per- fume his product. His procedure might be to compile a perfume specification and duly invite say six perfumers to submit a sample as tender. Prestonably the perfume specification indicated any price limit the manufacturer wished to impose. If all six perfumers submit tenders, the manufacturer needs to choose between six perfumes, Sx, S2, S3, S4, $5, So for his product. It appears a common method employed to make this choice is to use a consumer panel. Here a team of 30 or so individuals are requested to give their opinion and preference on the samples Si, and a particular one $* selected on the basis of this information. Such a process has the attraction of being simple to operate and also of avoiding any real decision on the part of the manufacturer in a highly subjective area. Panel tests An obvious question here is how one would recognize a good choice of $* and also what is expected of it? Before we discuss these points further, it will be useful to consider some possible problems associated with a panel test of the type described above. We shall assume each and every member of the panel to be a coherent individual capable of giving an informed opinion. Being coherent individuals, their preferences are transitive in that if S•PSj and SjPS•, then S•PS•, where P denotes preferred to. Suppose three firms A, B and C have submitted perfume tenders, and the preference orderings of a seven man panel is as follows:

174 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS Panel member 1 A 2 A 3 A 4 B 5 B 6 C 7 C P B P C P B P C P B P C P A P C P A P C P B P A P B P A A A A B B B B P B P B P B P A P A P A P A three samples two sam ties Now, if N(Y) is the number of times perfume Y is the most perfumed choice, and the group decision is made on the basis of the highest value of N(Y), with some further criterion for decision in the case of a tie, in the above case with three samples we have, N(A)= 3, N(B) =2. N(C)--2 Accordingly perfume A is selected out of the set A, B and C. If, however, only two samples are considered by the panel, say A and B, we see from the second table above which is obtained by deleting perfume C from the first table, N(A) = 3, N(B) = 4 and so B would be chosen from the set A, B. In short, even though each member of a panel is coherent, it is possible for a group decision procedure to be incoherent. As a further example of the kind of problem that can arise in group decision-making, consider the following three panel member, three product problem Panel 1 A P B P C member 2 B P C P A 3 C P A P B Let the mechanism for producing a panel choice be as follows: each indi- vidual ranks the alternatives as shown: for each pair (X, Y), the number N(X,Y), being the number of times perfume X is preferred to Y, is deter- mined: the alternatives for the panel are then ranked on the basis of the numbers N(X, Y). We find that N(A, B) = 2 N(B, C) = 2 V(C, A) = 2 N(B, A) = 1 N(C, B) = 1 N(A, C) = 1