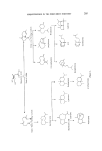
DECISION ANALYSIS 165 Zx - one environment X X: R:• ----- 14 Xa Ra• = 16 Xa R =18 optimum R/j - Xa R: =13 therefore decision is X• Ra•= 6 x, = (A, B, C) X• = (8, A, C) X• = (C, A, B) x2 = (A, C, B) X• = (B, C, A) X• = (C, B, A) Decisions under uncertainty Decisions are sometimes made in a situation in which environments can be identified, but nothing is known as to the likelihood or probability of a specific event pertaining. To be specific, consider a cosmetic company who have produced an innovatory skin preparation. Suppose they are considering the price at which to market the preparation, but as yet have no ideas as to the likely market response, that nothing like it has been marketed before and, as yet, no consumer test has been conducted. Management may be willing to consider themarketresponse (environments) on a three-point scale, poor, average and good. Suppose further the strategies are to market the product in one of three sizes at a cost of oe2, oe1.50 or oe1, and also, associated with these strategies and environments, an estimate of the likely profit over a year has been established as follows. Strategy Profit (suitable units) Good Average Poor x• (oe2) 7 3 X2 (oe1.50) 3 4 4 x• (oeD 4 2 Hence the decision-maker has to choose between the policies Xx, .Y• and X3 knowing nothing whatsoever as to the likely market response. Clearly the headings good, average and poor may be erased at this point since they communicate no usable information. Assuming the objective is to maximize profit over the year, how is the choice to be made? Laplace's criterion for this choice is based upon the Principle of In- sufficient Reason. Here there is no reason to suppose one environment any

166 JOURNAL OF THE SOCIETY OF COSlVIETIC CHEMISTS more or less likely than the other. This being so, environments are assumed equally likely and strategies accordingly measured by the average outcome across the environments. Thus we have Xx N 11.5/3, X2 N 11/3, Xa • 11/3 and Xx is accordingly chosen. There are many other ways of making this selection. Each policy could be viewed in terms of its worst possible outcome, in which case X2 would be chosen since it has the best worst outcome. This procedure of choice is the pessimist's criterion of Wald. Of course, one could equally well make the choice on the basis of the very best possible outcome, or a mixture of the best and worst outcomes. One selection criterion of interest to us here is that due to Savage- minimax regret criterion. The selection is made on the basis of the policy with the minimum maximum regret where, for each environment, regret is measured as the difference between what was obtained and the best that could have been obtained had the environment been known. For the above problem, we have for the regrets: Regret Good Average Poor Max regret 3.5 3.5 1 4 0 3 The chosen strategy is here Xa since it has the minimum maximum regret. Now suppose initially market prices of oe2 and oe1 are considered. If the decision-maker were to choose on the basis of Savage's criterion, the price would be fixed at oe2. However, we have just seen using the same criterion to choose between oe2, oe1 and oe1.50, the choice is oe1. This irrational behaviour is caused by the criterion concerned being non-transitive. Transitivity, sometimes referred to as coherence, is a very important concept in decision analysis. A decision-maker's preferences are transitive if, when A is preferred to B, and B preferred to C then A is preferred to C. With this condition unsatisfied, the decision-maker has no best choice between A, B and C. Few business men would be content to make decision under conditions of uncertainty. Most likely they would attempt to obtain further informa- tion as to the prevailing environment. This leads to a situation of risk. Decisions under risk In the case of decision-making under risk, the decision-maker assigsn probabilities to each of the environments indicating his degree of belief that