JOURNAL OF COSMETIC SCIENCE 94 The following example demonstrates how to determine the wavelengths that in refl ection are either constructively or destructively interfered for light that is normal incident from air on a thin fi lm with a refractive index of 2.5 and a thickness of 255 nm. Solution. For normal incidence, θ2 = 0. The pathlength from equation 13 is then 2 × 2.5 × 255 × Cos(0) = 1275 nm. Use constructive interference equation 14 and plug in various values of m and solve for λ1: ( )λ ( ) ( ) 1 2 1 1 1 2 1 1 1 2 1 1 1 1275 850 2 1275 λ λ λ λ λ = = = = = = 1275 2550 nm nm 5 510 3 1275 364 1 2 1 1 nm nm ( ) .29 λ λ = = Use destructive interference equation 15 and plug in various values of m and solve for λ1: ( ) ( ) .5 ( ) 1275 1275 2 1275 637 3 1275 425 1 1 1 1 1 1 λ λ λ λ λ λ = = = = = = nm nm n nm ( ) .75 4 1275 318 1 1 λ λ = = TRANSMISSION INTERFERENCE Transmission interference (WT) also results at point D in Figure 14 when the refracted portion of W I2 meets the internally refl ected portion of W I1 . These two waves will con- structively interfere if they are in phase. Since neither wave has refl ected off an interface where n2 n1, neither wave is phase shifted. Therefore, the net pathlength difference for W I1 must be λ. Thus the equation for constructive interference is in equation 16: …) 1 2 2 m 2n dcos (m 1,2,3,4 λ = θ = (16) Destructive interference of these two waves will occur if they are out of phase by 180 degrees. Again, neither wave has a phase shift of 180 degrees therefore, the net pathlength difference for W I1 must be 1 /2λ. So then, the equation for destructive interference is in equation 17: …) 1 2 1 2 2 (m ) 2n dcos (m 0,1,2,3 λ = θ = (17) The following example demonstrates how to determine the wavelengths that in transmis- sion are either constructively or destructively interfered for light that is normal incident from air on a thin fi lm with a refractive index of 2.5 and a thickness of 255 nm. Solution. For normal incidence, θ2 = 0. The pathlength from equation 13 is then 2 × 2.5 × 255 × Cos(0) = 1275 nm. Use constructive interference equation 16 and plug in various values of m and solve for λ1: ( ) ( ) .5 ( ) 1275 1275 2 1275 637 3 1275 1 1 1 1 1 1 λ λ λ λ λ λ = = = = = = nm nm 425 n 318.75 nm ( ) 4 1275 1 1 λ λ = =

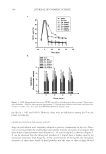
BASIC OPTICS OF EFFECT MATERIALS 95 Use destructive interference equation 17 and plug in various values of m and solve for λ1: ( ) ( ) ( ) 1 2 1 1 1 2 1 1 1 2 1 1 1275 2550 1 1275 850 2 1275 λ λ λ λ λ λ = = = = = = nm nm 5 510 3 1275 364 1 2 1 1 nm nm ( ) .29 λ λ = = CONSERVATION OF ENERGY One may have noticed that the solutions to the preceding examples for refl ection and transmission have an inverse relationship. The condition for constructive interference in refl ection is the same as for destructive interference in transmission, and the condition for destructive interference in refl ection is the same as for constructive interference in trans- mission. Energy is neither created nor destroyed by interference, it is just redistributed. Two waves interfere and two waves result, as in equation 18: W W W W I I R T 1 2 + = + (18) In other words, for cases where all layers are non-absorbing, then what is not refl ected is transmitted. This inverse relationship between refl ection and transmission gives rise to complementary colors. COLOR FROM INTERFERENCE White light contains a continuum of wavelengths from 400 to 700 nm. For simplicity, white light can be broken down into the three primary colors and assigned an average wavelength: blue = 450 nm, green = 550 nm, and red = 650 nm. In Figure 15, the in- tensity of each of the three primary colors is plotted versus pathlength difference. The maxima and minima for each primary color correlate to the conditions for constructive and destructive interference, respectively. Conditions for constructive interference occur when the pathlength difference equals 0.5λ and 1.5λ, etc., and destructive interference occurs when the pathlength difference equals λ and 2λ, etc. For example, look at the curve for the blue primary. Here, 0.5λ and 1.5λ are 225 and 675 nm for constructive interference, and λ and 2λ are 450 and 900 nm for destructive interference. All other points on the curve represent some degree of partial interference. Note about the intensity values in Figure 15: The original wave in Figure 3 has an am- plitude of one. Upon constructive interference, the resulting wave has an amplitude of two (see Figure 8). The intensity is the square of the amplitude, thus resulting in four. Also note that Figure 15 applies to refl ection interference only. Of all the wavelengths in white light, only a few of the wavelengths are actually construc- tively or destructively interfered for a particular fi lm, with the rest being partially inter- fered. The observed interference color of a particular fi lm is then the combined effect of adding the partial interferences plus the few constructive and destructive ones. The sim- plifi ed primary colors in Figure 15 also demonstrate this principle. Figure 16 highlights particular cases of pathlength differences. There are infi nite combi- nations of refractive index, fi lm thickness, and incident angle that can produce a given pathlength difference. For simplicity, the refractive index of the fi lm will be fi xed at 2.5,