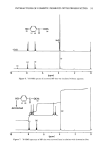
EXTENSION OF PERMED HAIR 127 H20 I REDUCTION H20 iH202 H20 I I ,Fo I TIME Figure 1. Idealized representation of an experimental curve obtained during static and dynamic extension testing of a hair fiber subjected to reduction/reoxidation treatment. After the second rinse for time (t 5 - t4) of 5 min, the fiber was released and within 1 min again strained to ß 1%. The initial length of the fiber 10 and its set length 11, i.e., its length after the treatment, were determined by extrapolating the stress strain curves to zero stress (Figure 1). The testing procedure ensures a basically infinite liquor/hair ratio and therefore constant conditions during all treatment steps. In practice this ratio rarely exceeds 2:1 (2). In all cases the time of reduction was set to approach an apparent steady state for the static stress and, hence, for the reaction of the reducing agent. To determine the fiber-bending set, hair fibers were wound around PVC cylinders of 12-mm diameter under a weight of 200 mg and their ends fixed with drops of nail polish. Care was taken that the plane formed by each fiber loop was perpendicular to the cylinder axis. The cylinders were suspended in a beaker and treated under the same conditions as for the extensional measurements. After the final rinsing step, the cyl- inders were removed from the beaker. The loops were cut without delay and dropped into a petri dish containing distilled water (20øC). The diameters of the loops were measured with a ruler within 1 minute and again after 16 hours. MECHANICAL CONSIDERATIONS Set during a permanent waving treatment is produced by deforming the hair and cleaving some of the sulfur crosslinks which then reform in the deformed state by reoxidation or by thiol-disulfide interchange. The crosslinks formed in the new configu- ration enforce at least a partial retention of the hair deformation. The permanent set of the bending deformation thus achieved is analogous to the cohe-

128 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS sive set of a hair that is induced by the breaking and reformation of hydrogen bonds. Cohesive set is achieved by wetting and subsequent drying of a hair in the bent state. Though the mechanisms of the impartation of permanent and cohesive set are different, involving either covalent or secondary bonds, the analogy of the mechanisms involving bonds that can break and reform suggests an analogous theoretical approach. The laws of the formation and the recovery of the cohesive set are governed by the general principles of linear viscoelasticity. Chapman (7) has shown that the set of a wool fiber can be predicted from its relaxation behavior by a generalized theory of viscoelas- ticity. Denby (8) developed an approximation to calculate the time-dependent recovery of a bent wool fiber from its relaxation behavior that holds well for slow relaxation processes. Denby's equation for the calculation of fiber recovery, R, in its simplest form is given by: and the related set generally as: R = B(t)/B(t-w) (1) s = 1-R (2) B(t) is the time-dependent flexural stiffness of the wool fiber at any time, t, after the initial deformation at time t = 0. The fiber is released at t = w, and B(t-w) is the bending stiffness of the same fiber during the time of release. Omitting the time dependence of recovery, the initial recovery R o of the permanently waved fiber in analogy to equation 1 is given by: Ro = BrdBro (3) Bre is the residual of the initial bending stiffness of the deformed fiber after the treat- ment (the suffix "re" stands for "reduced"), and Bro , the new bending stiffness of the reoxidized fiber (the suffix "ro" stands for "reoxidized"). The implication of equation 3 parallels the practical observation that the set of a curl increases with the degree of softening of the hair, that is, with the progressing decrease of the initial stiffness Bre and with the completeness of the reoxidation, so that the bending stiffness after the treatment Bro is as close as possible to the initial value. The bending and extensional properties of a hair can be interrelated by straightforward mechanical principles. Assuming that extensional and compressional properties are equal, the flexural stiffness, B, of a hair and its Young's modulus, E, are related by: B = El (4) where I is the moment of inertia of the cross-section of a circular fiber given by: I = q-r d4/64 (5) and d is the diameter of the fiber. Since the bending stresses enforcing and those opposing recovery act on the same fiber cross-section, equation 3 can be modified by inserting equation 4 to yield: R o = Ere/Ero (6) Ere is the residual of the initial relaxation modulus proportional to the static stress level