EXTENSION OF PERMED HAIR 137 M is small in water and relaxes (within feasable experimental time limits) to an extent that the equilibrium modulus is approached (Figures 2-5). This modulus amounts to about 80% to 85% of the initial modulus (Figure 6) and is the contribution of the or-helical filaments to the overall fiber modulus. From an experimental point of view, it follows that the initial difference between the relative static and dynamic forces in water of about 15% is the contribution of phase M to the dynamic modulus. Considering the concept of the dynamic and the static modulus for rubber, as outlined by Tobolsky (4), there are two possible mechanisms that can affect the apparent contri- bution of phase M during reduction, and these processes have opposing effects. First, any back reaction of the reduction will decrease the number of sulfur bonds broken in the hair fiber at any given time and will increase the dynamic compared to the static modulus, and will hence increase the difference between the moduli. Second, the con- tribution of phase M to the static modulus is removed by stress relaxation, so that the difference between the dynamic and the static modulus is the dynamic modulus of phase M. Any effect of sulfur bond fission on the mechanical properties of phase M will decrease its dynamic modulus and therefore decrease the moduli difference. As outlined in Results, no significant change of the difference between static and dy- namic moduli occurs on reduction with 0.3 M TA, 1 M Cys-HC1, and 1 M sulfite. Either the properties of phase M are unchanged by the reduction or the effects of the two mechanisms that can induce a modulus change cancel each other. Assuming the invariance of the phase M properties, it follows that the reduction reactions all occur, as was to be expected, without any substantial back reaction, i.e., without reformation of broken sulfur bonds that contribute only to the dynamic modulus. Basically all sulfur bonds that are broken stay broken in the presence of the reducing agent. For 1 M TA the moduli difference, and hence the modulus of phase M, vanishes on reduction, indi- cating that rather severe conditions are required for the mechanical properties of phase M to be significantly affected. For all cases the main effect of reduction is on the contribution of the crystalline fila- ments, and it is the change of their properties that induces permanent fiber set (6, 14). It is likely that the helices themselves, as crystalline structures, are not affected by reduction (19), but rather the interactions between helices, which also rely on disul- phide bonds, are affected (17). Feughelman's model for the filaments in ot-keratins (20) proposes that the or-helical units are short so that any disruption of their interaction would lead from a contin- uously reinforced material towards a short-fiber composite, with the consequence of a significant decrease of the fiber modulus (21). During reduction a fraction of the sulfur-based interactions between the or-helical units is broken and the static modulus decreases. When the interactions are reformed, fila- ments are generated and their equilibrium state is the deformed shape. These filaments contribute to the modulus Ero that opposes redeformation and, hence, recovery. Ere is a measure of the amount of filaments or of the fraction of the original filament modulus that still supports the original form. On rinsing, the static force level stays constant since any stress-free, reformed sulfur bond in the related reformed filament whose equilibrium state is the deformed state will not contribute to the static force level. The dynamic force rise during rinsing indicates the shift of the equilibrium towards the sulfur bond reformation when the reducing

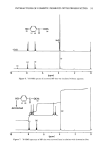
138 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS agent is removed and a possible contribution of sulfur bonds that are reoxidized by the oxygen contained in the water used for the rinse (15). A consequence of this effect is that substantial set of a wave can be expected just by rinsing the hair. The final gain of Ero is achieved by reoxidation. As outlined in Determination of Fiber Set, equation 6 directly applies to the longitu- dinal properties of the fiber and, according to DeJong's work (6), should give an accu- rate prediction of the length set acquired by the fiber due to treatment. Nevertheless, the data suggest that a hair fiber cannot, at least under the conditions applied, be chemically set at small extensions (½ 2%). Considering the values in Table I, S L in no case comes close to the set predicted, even though the actual bending set is greater than predicted. For all conditions, even cases of negative set, that is a length contraction on release, were observed and the value zero is always included in the 95% confidence limits of the mean of S L. The initial bending set of a fiber will always contain a fraction of cohesive set due to the initial modulus of phase M. The recovery increases with time since the phase M mod- ulus decays rapidly in water and cannot maintain its contribution to the fiber set for any prolonged period of time. The ratio Ri/R•6 = 0.8 (Table II) confirms the applicability of equation 7 and the expectation •(oo) = 0.8 (see Mechanical Considerations). The contributions of phase M to the fiber set are (independent of treatment) accounted for by the introduction of the relaxation function. After the reduction/reoxidation se- quence, the contribution of phase M to the fiber modulus is basically unchanged in accordance with DeJong's (6) observations, and, as the data would indicate, even stays unchanged during the reduction, with the 1 M TA treatment as an exception. Hence it would appear that the properties of phase M have no bearing on the differences between anticipated and measured fiber recoveries and on the limits of the applicability of equa- tions 6 and 16. Figure 7 shows the relation between the measured and the calculated recoveries of bending set. In all cases the recovery observed experimentally is significantly lower than predicted. The systematic difference between R i and R o shows that there appears to be a satisfactory correlation between the prediction and the experiment that can be used to assess, at least on a comparative basis, the efficacy of a treatment. Nevertheless, an accurate prediction based on the interrelation between bending and extensional proper- ties does not seem to be possible. The nature of the difference between the recovery values indicates that other mecha- nisms besides the change of the extensional modulus must be operative for set determi- nation. The nature of this mechanism can possibly be understood by assuming that during diffusion the reducing agent decreases in concentration through the reaction with the sulfur cross-links in the fiber, leading to a continuous decrease of the degree of reduc- tion from the fiber surface towards the fiber core. In consequence, while the measured extensional modulus of the fiber reflects the resulting effect of the reaction over the whole fiber cross-section, the true modulus Ere of the outer parts of the fiber might be considerably lower than the modulus near the center of the fiber. Since the outer parts of the fiber contribute more towards the bending stiffness of the fiber than the inner parts, as expressed by equation 5, a decrease of Ere in the outer parts of the fiber compared to the average value of Ere , as obtained from the extensional measurements,