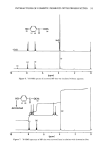
EXTENSION OF PERMED HAIR 129 reached in the strained fiber after reoxidation (t t4). Ero is the initial, i.e., the Young's modulus of the reoxidized fiber. It is important to mention that the step from equation 3 to equation 6 via equation 4 is only justified if the moduli are uniform over the whole cross-section of the fiber. In the view of this approach, any deviation between the calculated and the measured recovery would be a measure of the inhomogeneity of the radial distribution of the modulus which might arise from inhomogeneity of the degree of reduction within the fiber (see Discussion). The stress of a wool fiber in water (20øC) at small strains (½ 2%) relaxes and ap- proaches an equilibrium stress of about 80% of the initial value within 20-30 min (9, 10). This time-dependent fraction of stress in the strained fiber is removed during the course of the chemical treatment of a deformed fiber, so that Ere, the modulus attained by the fiber after physical and chemical relaxation, is expected to be constant with time. E•o is the modulus in equilibrium with the deformed state and hence relates to the unstrained fiber. Under the internal fiber strains, during recovery, E•o is subject to the usual stress relaxation of a wool fiber due to hydrogen bond cleavage that will increase recovery by removing the cohesive fraction of set in the fiber. By analogy to the approach by DeJong (6), this time dependence of the cohesive set can be accounted for by introducing the relaxation function •(t) into equation 6, yielding for the time dependence of recovery: R(t) = E•e/[Ero xlt(t)] (7) Considering the stress relaxation of a wool fiber in water, the relaxation function is expected to decrease towards an equilibrium value of •(oo) = 0.8. Experiments have shown that equation 7 properly accounts for the equilibrium contri- bution of cohesive effects to recovery, though it is unsuitable for the description of the time dependence of these effects. The time dependence of the removal of cohesive set from permanently waved fibers is the object of further investigations. EXPERIMENTAL CONSIDERATIONS AND DATA EVALUATION Tobolsky (4) reviewed some principles of dynamic and static relaxation tests for the investigation of the permanent deformation of rubbers that relax through thiol-disulfide interchange. The relaxation of the stress in a fiber at constant strain is a measure of the cleavage of those bonds that stabilize the undeformed state. The remaining stress at the time of release after fiber deformation, stress relaxation, and fiber treatment is a measure of the fraction of the initial interactions that at time t = w still oppose the deformation and hence enforce recovery. The change of the dynamic stress at constant dynamic strain reflects the net effect of the bonds broken and the bonds reformed during the treatment. The dynamic stress after reoxidation and during the final rinse is related to E•o, the modulus of the fiber after treatment which is in equilibrium with the deformed state. Figure ! shows schematically the force-time diagram produced during the experiment. The initial modulus Eo of the fiber, assuming elastic behavior is given by:

130 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS E o = Fd(e s A o) (8) F o = force at the end of the straining step. ½s = initial static strain. A o = initial cross-section. The dynamic modulus at any time during the treatment Ea(t), normalized for the initial cross-section of the fiber, is given by: Ea(t) = AF(t)/(½ a Ao) (9) where AF is the difference between the peak force reached during the strain pulse and the force level of the base line, given as a broken line in Figure 1. ca is the magnitude of the strain pulse. For the untreated fiber in water at t tt, the initial dynamic modulus Eao is given by: Eao = AFo/(½aAo) (10) The difference that is observed between the initial modulus E o and the dynamic mod- ulus Eo a at equal strain rates can be attributed ro fiber crimp and to experimental influ- ences, that is, a certain deviation from perfect alignment in the experimental set-up that can never completely be avoided, so that: E o = k E• (11) with k 1. After the treatment, during the last rinse, and prior to release, the residual Ere of the initial modulus Eo, again normalized for A o, is given by: Ere •= E(t) = F(t)/(½ s Ao) for t • t 4 (12) Similarly, the dynamic modulus of the reoxidized fiber is given by: E•ao = Ea(t) = AF(t)/(½ a Ao) for t • t 4 (13) where E•ao is the dynamic modulus of the fiber in' the reoxidized state, yielding with equation 11 the initial modulus in the reoxidized state Ero as: Ero = k Erao (14) Equations 12, 14, and 13 are successively inserted into equation 6. Subsequently, the upper and the lower parts of the resulting equation for R o are both normalized by dividing by E o. Equations 11, 10, and 8 are introduced, yielding: R o = (F(t)/Fo)/(AF(t)/AFo) for t t 4 (15) Equation 15 states that the degree of fiber recovery depends on the interaction of the normalized static and dynamic forces after the treatment and during the final rinse, relative to the initial undeformed state of the fiber. With respect to the conditions of equation 6, equation 15 reads as: R o = (Fre/Fo)/(AF•o/AFo) (16)