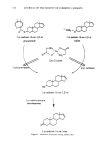
178 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS Log Standard Deviation 0.225 + 0.200 0.•75 + 0.150 0.125 0.100 0.075 0.050 + + A A AB A A A A A A A A A A AA A AA A AA A A A A BA A B AA AA A A A A B A B AAA BA AAA ADC AAA AAA A A A B A B B A A B A AAAAA B AA A ACBA B A AAA AAB AAAB AA A A A A A AAA A B AB A A A A A A A 0.025 0.1 2 O. Mean Log Sweat Ratio Figure 8. Test subject baseline axillary log(right/left sweat ratios): Plot of standard deviation versus mean by subject. •jkmi) is N (0, (•2), independent for all i, j, k, m, with d/)i(i) and ½ikm(i) mutually independent. The first step in the statistical analysis of antiperspirant test data is analysis of variance (ANOVA). This procedure assesses the statistical significance of the three fixed-factor effects, treatment, sides, and treatment by sides interaction (groups) on the response, log sweat rate. The random effects, subjects and axillae, provide the estimates of variability needed to test for the existence of the fixed effects. For split plot designs, the analysis of variance procedure comprises the "whole plot" analysis, calculations that depend only upon the sums of the log sweat rates of the two axillae of each subject, and the "split plot" analysis, calculations that depend only upon the differences between the log sweat rates of the two axillae of each subject. The statistical test for the treatment by sides interaction is within the whole plot analysis. This interaction effect is aliased with groups and is tested against the whole plot error, which is the variation in subject sweat rate totals within groups. The sides and treatment effects are evaluated in the "split plot" analysis. These effects are tested against the residual error. The residual error used as the split plot error is the variation of axillary log sweat rate differences of subjects within groups. To summarize the analysis of variance procedure, we exhibit the ANOVA table shown

ANTIPERSPIRANT RESULTS 179 below, based on n• subjects allocated to Group 1, and n 2 subjects to Group 2. The calculations for the split plot analysis of variance can be found in most standard texts, such as Cochran and Cox (7), Milliken and Johnson (8), and Winer (14). Source of Degrees of Sum of Mean F Test variation freedom squares squares statistic Whole plots Mean 1 SSM MSM MSM/MSS Groups* 1 SSG MSG MSG/MSS Subjects (groups) n• + n 2 - 2 SSS MSS Split plots Sides 1 SSL MSL MSL/MSE Treatments 1 SST MST MST/MSE Residual n• q- n 2 -- 2 SSE * Aliased with treatment by side interaction. An unusual feature of this design is that the interaction is in the whole plots, and both of the main effects are in the split plots. (In most textbook examples one factor is assigned to the whole plot units and the other factor to the split plot units, with the interaction in the split plots.) STATISTICAL DESIGN AND ANALYSIS OF MULTITREATMENT STUDIES For multiple treatments, a number of experimental designs are available, based on test objectives. The test panel is divided into "cells," each cell corresponding to a pair of treatments. Each cell is then subdivided into two groups as described for the two- treatment case. Subjects are randomly allocated to cells and groups within cells. These designs are in the general class of "incomplete block" designs, described in many textbooks such as those by Cochran and Cox (7) or Milliken and Johnsor, (8). Of particular interest in antiperspirant studies are two designs, which we have termed the round robin (RRB) and each versus control (EVC) designs. If equal information is desired on all comparisons between pairs of treatments, the RRB design is used in which the number of cells is equal to the number of pairs of treatments. This is termed a "balanced incomplete block" design in the statistical literature. If, for example, there are three treatments, A, B, and C, then the three cells correspond to the three pairs AB, AC, and BC. The table below lists the number of cells and groups in a round robin design versus the number of treatments. Number of treatments, t 3 4 5 6 7 Number of cells, t(t - 1)/2 3 6 10 15 21 Number of groups, t(t - 1) 6 12 20 30 42 This places an obvious lower limit on the number of subjects in the panel for a given number of treatments, since at least one subject is required per group. It is desirable to have more than one subject per group to cover "drop-outs." The EVC design is applicable when three or more treatments are to be compared, and one of the treatments is to be singled out as the control treatment. The remaining treatments are termed the test treatments. Each subject receives the control treatment on one axilla and one of the test treatments on the other axilla. The EVC design has t - 1 cells, where t is again the number of treatments.