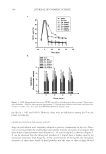
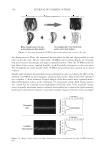
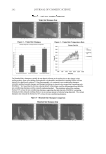
J. Cosmet. Sci., 61, 85–105 (March/April 2010) 85 Basic optics of effect materials STEVEN A. JONES, BASF Corporation, 540 White Plains Road, Tarrytown, NY 10591. Accepted for publication August 24, 2009. Synopsis Effect materials derive their color and effect primarily from thin-fi lm interference. Effect materials have evolved over the decades from simple guanine crystals to the complex multilayer optical structures of today. The development of new complex effect materials requires an understanding of the optics of effect materials. Such an understanding would also benefi t the cosmetic formulator as these new effect materials are intro- duced. The root of this understanding begins with basic optics. This paper covers the nature of light, inter- ference of waves, thin-fi lm interference, color from interference, and color travel. INTRODUCTION Classical color pigments produce color by absorbing select bands of the visible spec- trum. The remaining wavelengths are diffusely refl ected (scattered) and combine to produce a color. Many effect materials, on the other hand, derive their color from thin fi lm interference. Examples of products that contain thin fi lms include mica and boro- silicate fl akes coated with TiO2 and/or Fe2O3, and more recently with multilayer stacks such as TiO2/SiO2/TiO2. As a result of refl ection and refraction of light on a thin fi lm, certain wavelengths are removed by destructive interference while others are enhanced by constructive interference. This paper provides an understanding of how light interacts with a thin fi lm to create interference and how color is derived from that interference. NATURE OF LIGHT LIGHT AS A WAVE In physics class, we are taught about the dual nature of light, sometimes being consid- ered a particle and at other times a wave. For the purposes of thin fi lm interference, light is considered to be a wave as depicted in Figure 1. A wave has a wavelength λ, which is the length of a repeating unit (m) shown in Figure 1, a velocity v, which is the speed of the wave in a medium (m/s), and a frequency ν, which is the number of waves that pass per unit of time (s-1 or Hz). Wavelength, velocity, and frequency are related by equation 1: