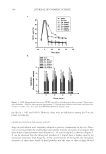
JOURNAL OF COSMETIC SCIENCE 86 = Qλ v (1) It is important to note that the frequency is fi xed by the light source and remains con- stant. Also note that wavelength and velocity are directly proportional and that wave- length and frequency are inversely proportional at constant velocity. For a wave traveling in a vacuum or in air (close enough to a vacuum), the velocity is c, and the speed of light, 3 × 108 m/s. INDEX OF REFRACTION The index of refraction is a unitless complex number (n + ik), where k is the absorption coeffi cient. For transparent, non-absorbing materials, k = 0 and the refractive index re- duces to the simpler and more familiar n. The refractive index of a medium is defi ned as the speed of light in a vacuum divided by the velocity of light in the medium, as in equa- tion 2: n c v = / (2) The higher the index of refraction of a material, the slower the velocity of light through the material. The refractive index of a material is also dependent on the wavelength of the light. For white light, which contains many wavelengths, this phenomenon is referred to as dispersion. Therefore, tables of refractive indexes list values for one wavelength, com- monly 589.3 nm, also referred to as the sodium D line. REFLECTION AND REFRACTION When light travels in a medium, it travels in a straight line until it hits an interface, defi ned as a change in the refractive index. At the interface, some of the light is refl ected and some is refracted (see Figure 2). The law of refl ection states that the incident angle relative to the normal, θ1, is equal to the refl ected angle, θ1′. This refl ection is specular. If the refl ection is at an interface where n2 n1, the refl ected wave has a phase shift of 180 degrees. The percentage of light Figure 1. A light wave of wavelength λ.

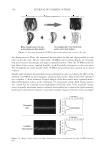
BASIC OPTICS OF EFFECT MATERIALS 87 refl ected at the interface is determined by the Fresnel equations. At normal incidence, the Fresnel equation simplifi es to equation 3: R n n n n 2 1 2 1 2 = − + [( )/( )] (3) The equation becomes more complicated for non-normal incidence. Regardless of the form, the point is the same: the larger the difference between n1 and n2, the higher the refl ection will be. For example, at the interface between media with an index of refraction of 1 (air) and 2.7 (rutile titanium dioxide), the % refl ection (at normal incidence) is 21%, while the % refl ection (at normal incidence) at the interface between media with an index of refraction of 1 (air) and 1.5 (silica) is only 4%. Light that is not refl ected at the interface enters the medium and is refracted. The refrac- tion angle θ2 is determined by Snell’s law in equation 4: n Sin n Sinθ 1 1 2 2 θ = (4) The velocity of light through a medium that is denser than space (or air) is slower than the maximum value for the speed of light. Equation 2 can be rearranged to solve for ve- locity as in equation 5: v c n = / (5) This equation means that the higher the refractive index of a medium, the slower the velocity of light through that medium. If equation 5 is substituted into equation 1, the result is equation 6: c /n = νλ (6) Since the frequency of a wave and the speed of light remain constant, the wavelength of light changes according to equation 7: λ λ 2 1 1 2 n = ( / ) n (7) Figure 2. Refl ection and refraction of incident light at the interface between media with refractive indexes of n1 and n2.