j. Soc. Cosmet. Chem., 40, 173-189 (May/June 1989) A new approach to hair surface topography: Fourier transform and fractal analysis MAREK ZIELINSKI, Biophysics Department, Clairol Research Laboratory, 2 Blachley Rd., Stamford, CT 06922. Received November 23, 1988. Presented at the Annual Meeting of the Society of Cosmetic Chemists, New York, December 1988. Synopsis Geometrical properties of the hair surface, such as surface roughness, strongly influence its feel and appear- ance. Topological features of different orders of magnitude are present and are expected to influence the perceptible attributes to varying extents. Profilometry is an established method of studying the geometry of such surfaces. It has a resolution better than that of an optical microscope and lends itself to numerical analysis and quantification more easily than do the electron microscope images. The interpretation of the profile data, traditionally performed using metallurgical roughness parameters, is, however, inadequate and fails to correlate clearly with hair properties that depend on roughness. We here describe use of the tools of fractal geometry to interpret surface profiles of hair. The advantage of fractal geometry comes from the fact that topological features of the hair surface exist in every scale of magnification, extending over several orders of magnitude. We show that hair surfaces display a character- istic "roughness" on widely differing scales, and hence that the corresponding profiles can be interpreted as fractal objects. It follows that the fractal dimension of the hair profile line describes properties of the hair surface with controllable sensitivity. The spectral method using the Fourier transform is introduced for calculation of the fractal dimension. Whereas standard surface measures such as the "average roughness depth," Rz, depend strongly on the measuring length selected and are thereby restricted to a particular scale size, applicability of fractal geometry to hair surface analysis provides us with a more systematic approach that naturally encompasses all size ranges. Practical applications to measurement of natural and treated hair are presented. INTRODUCTION Surface properties of solid objects are the subject of a broad and diversified discipline, namely "surface science." Among the surface properties of interest are electrical, me- chanical, and optical properties adsorption, adhesion, catalysis, corrosion, friction, wear, and wettability. In this paper, we limit our interest to topographical analyses of surfaces, i.e., we will treat them as n-dimensional in a mathematical sense and disre- gard the material properties of the objects to which the surfaces belong. However, some implications of this analysis for physical properties of surfaces, such as adsorption or friction, will also be discussed. In the field of cosmetic science, the perceptible properties of skin and hair such as 173

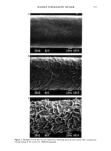
174 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS appearance, texture, feel, and softness are of greatest importance, since the effectiveness of products is judged upon these impressions. All these properties are strongly related to the geometry of the surface. Take, for example, appearance: in the case of hair we can talk of shininess and luster (or dullness), which are directly dependent on the way light is scattered on the hair surface. The light will be scattered most on the irregularities having the dimension of the light wave, while roughness on a large scale will affect the luster only slightly. Skin texture, on the other hand, although also related to elasticity, depends on the roughness discernible by feel and hence senses a larger scale size. Ad- sorption of surface-active substances onto the surface of hair is most important in treat- ment of hair with shampoos and conditioners. Total adsorption is proportional to the "specific surface area" of hair, which depends on surface irregularities that are of the order of the molecular dimensions of the adsorbate. Recently, significant progress has been made in characterizing the surfaces of skin (1-5) and hair (6) using profilometric techniques. Damage to hair due to various chem- ical and mechanical stresses has been the object of another study in which SEM observa- tions were used to assess the damage to the hair surface (7). The effects of aging, drugs, and various cosmetic treatments on surface roughness parameters have been derived from the digitized surface profiles. A number of different roughness measures were used, including metallurgical parameters, statistics of surface peaks, autocorrelation functions, and the Fourier transform, as well as some specially developed techniques. One common feature of these approaches is that the raw data were preprocessed or filtered before the analysis, using rather arbitrary procedures to remove any "unwanted" data. A common method of such filtering is the separation of "waviness" from "rough- ness," using either electrical or numerical techniques. Since, as we will show, morpho- logical structures of real surfaces appear on all scales, it is possible to arbitrarily ascribe the term "roughness" to any morphological feature or to filter it out entirely. Because each researcher uses his own filtering procedure, it is not surprising that the results do not show good agreement. It has been found (8) that Euclidean geometry, which deals with such "well behaved" geometrical figures as a plane or a circle, does not adequately describe the properties of such objects as coastlines, snowflakes, clouds, and also rough surfaces. In this study, we will discuss some fallacies of using Euclidean geometry to describe roughness. We will also explore the advantages of applying the new branch of mathematics, fractal geometry, for the characterization of rough surfaces in general and to the hair surfaces in particular. EXPERIMENTAL Surface morphology measurements were performed on hair samples using an industrial profilometer, model "Perthometer S6P" manufactured by Perthen GmbH, Goettingen, West Germany. Hair fibers were mounted on a glass slide using double-sided tape after the measurement, samples were inspected using a scanning electron microscope (SEM). The hair surface was measured longitudinally using a wedge-shaped stylus (Figure 1) profilometric scanning of the fiber surface was from root to tip, with the stylus slanted 5 degrees in the scan direction. The hair surface was not damaged significantly by the probe however, some traces of the probe's path were visible, as can be seen in the photograph shown in Figure 2. In most experiments, the scan length was 4.03 mm and