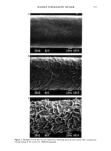
SURFACE TOPOGRAPHY OF HAIR 179 not. As we will show below, such profile is best described as a fractal object. For now let us note that roughness parameters such as Rz, Ra, and Rq are meaningless as a measure of roughness of the whole profile, since their value depends on the measured length. Roughness parameters only represent a property of a particular section of the profile. Scan length dependence of roughness parameters has been observed previously (6) and explained as being due to "increasing contributions from periodic or stochastic alter- ation of the hair surface." We will show that this dependence is a direct consequence of the self-similarity of the profile and is not related to any specific characteristics of any particular surface. FRACTAL GEOMETRY The term fractal is due to Benoit Mandelbrot (8), who coined this word to bring to- gether a large class of mathematical structures that did not fit well into the patterns of Euclidean geometry. Some of these objects were regarded as "pathological" or "mon- sters" by nineteenth century mathematicians, who invented them as examples of the richness in which mathematics can surpass nature. Only recently came the realization that these "monsters" are often the best models of the reality surrounding us (8). A fractal object in a plane, a fractal curve, has very strange properties: it has no slope at any point, and although it may have a beginning and an end, its length is indefinite. The better we approximate it, the longer it appears. An example of such a geometrical (regular) fractal is the Koch curve shown in Figure 6. Following Mandelbrot (8), we will construct it by the method of consecutive approximations. We start with a straight interval of length 1, called the initiator. We will then replace its middle third by an equilateral triangle the resulting second approximation is a broken line formed by four (N = 4) intervals, each equal to V3 of the initial interval (r = V3). This shape will be called the generator. Proceeding further, we will replace each of the four intervals of the generator by a new generator reduced in ratio by one third, and continue this process indefinitely. The final product of such operations, of which Figure 6a shows only the first five approximations, is a fractal object. Such construction using successive approximations is also not unusual in Euclidean geometry. Starting, for example, with an equilateral triangle and then increasing the number of sides in this regular polygon, we will obtain a circle as a limit of this Table I Dependence of Measured Roughness Parameters on the Length of the Scanned Section of the Hair Scan length Rz Ra Rq [mm] [p•m] [p•m] [p•m] 0.56 0.93 0.16 0.20 1.6 1.04 0.15 0.19 5.6 3.37 0.62 0.79 16.0 4.98 0.79 1.00 56.0 14.32 2.39 3.48 Average roughness depth Rz, average roughness Ra, and geometric average roughness Rq are mean values of four hair samples with three scans on each hair.

180 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS 1.3 4- 1.2 1.1 1 0.9 O.B 0.'7 0.6 0.5 0.4 0.3 0.2 0.1 0 -0.1 -0.2 -0.3 -0.1 0.1 0.3 O.S 0.7 0.9 1.1 1.3 1.S 1.7 Log (Measuring Length) Figure 5. The "average roughness depth" Rz measured for four different hair samples (four different symbols) and for measuring lengths varying from O. 3 mm to 30 mm. operation. The circle circumference is a finite number, however, while the length of the Koch curve is infinite. The circle is one-dimensional the dimension of the Koch curve is ca 1.26. Further discussion of the principles of fractal geometry is presented in Ap- pendix 3. FRACTAL MODELS OF ROUGH SURFACES We propose to use fractal objects as models of biological surfaces, hair in our case. In the first approximation, one could use the Koch curve as a model of the surface profile. The Koch curve is, however, too regular to be a serious representation of any of the profiles shown in Figure 4. A better approximation of the hair profile would be a trace of Brownian motion (9) or the random Weierstrass-Mandelbrot function (10). Fortu- nately, we do not have to fit a particular function to obtain statistically significant information. We will only attempt to determine the measure of the profile "fractality," its fractal dimension D (8). The curve having fractal dimension D = 1 is a "smooth," differentiable line. The fractal curve of dimension D = 2, such as BrownJan motion, fills the plane completely. As D increases above one, the line becomes more and more