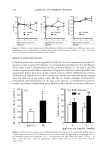
EFFECT OF HAIR COLOR ON LUSTER 429 Luster values as a function of dyeing time under monochromatic illumination are shown in Figure 4. For all dyes the increase in luster with dyeing time was low. Most changes in luster occurred between zero and five minutes dyeing time, similar to changes observed in reflectance spectra. During this time basic dyes penetrated the cuticle and deposited on the fiber surface. From five minutes to 45 minutes the change in luster was smaller. Even though the HC dyes penetrated into the cortex during this time, they were not sufficient to reach sorption equilibrium (15). Thus, changes in luster with dyeing time are similar to those of reflectance spectra and are related to the different affinities and different time-based dyeing characteristics of semipermanent dye components. For all colors we noticed that with increasing dyeing time the diffuse peaks were weaker and the resolution of the specular and diffuse peaks was better, which resulted in increased luster values. The increase in luster with increase in coloration, and thus with dye concentration in the fiber, can be explained by a simple optical model for light reflection from hair fiber, shown in Figure 5. When light with an intensity of I o impinges on a hair fiber with an angle of incidence of 45 ø , several processes such as reflection, absorption, and scattering occur. The conservation of light can be expressed as follows: •0 = IR q- IAB q- ISC q- IOUT (2) where I R is the intensity of reflected light, lAB and Isc are intensities of absorbed and internally scattered light, and lou T is the intensity of transmitted light, i.e., lost from the back side of the fiber. The first term in equation 2, IR, contains reflections with different origins: = Ix. + Io,FF(x) + IO,F(,NT) (3) 28 26 24 õ 2o 18 16 14 12 Red Green Blue 0 10 20 30 40 50 Dyeing time (min! Figure 4. Luster calculated from goniophotometric curves for various dyeing times for different semiper- manent colors. Measurements were performed under He-Ne laser beam illumination (k=632 nm).

430 JOURNAL OF COSMETIC SCIENCE lOUT IAa+Isc Iolvv(s) Isp IDIFF(INT) IAs+Isc Figure 5. Geometrical and physical optics of light interacting with a model cylindrical fiber. where Isp is specularly reflected light from the surface of the fiber, ID•FF(SR) is the diffusely reflected light resulting from surface roughness, and ID•Fm•NT) is the compo- nent of diffusely reflected light coming from the reflected beam from the back side of the fiber. Io•m•NT) depends greatly on the internal structure of the fiber and its absorptive and scattering behavior. By introducing equation 3 into equation 2, the expression for luster can be rewritten as: Isp Isp L = (isv + IDWV(SR) + iDWV(,NT)) = I0 _[AB -- ([SC .qu [OUT) (4) It should be noted that both IDWV(•N•) and Iou • are functions of lAB and Isc. Also, lAB and Isc are interdependent. If absorption is dominant, then scattering Isc + Iou • is considerably reduced. Equation 4 can be used to interpret luster changes of a fiber substrate based on absorptive and scattering processes. Since specular reflectance is a surface phenomenon and is essentially independent of hair color, the luster given by equation 4 is controlled by the denominator. If lAB is large, the amount of diffusely scattered background light is very small. The small denominator gives high luster. IflAB is small, Isc is larger and the light scattering in the fiber interior occurs in multiple directions, which gives a diffuse background. The denominator is larger and luster is lower. The refractive index plays an important role in controlling both the Isc and Iou •. Thus, absorptive processes play a dominant role in controlling the denominator of equation 4 and luster. This explanation is both true for colored hair, where the absorp- tion of light arises from the dye molecules in the fiber interior, and for naturally colored hair, where absorption is by melanin granules. The effect of dyeing time on luster can be explained by equation 4, since absorption and scattering depend on the type of dye (extinction coefficient) and its penetration and distribution into the fiber.