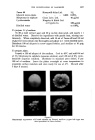
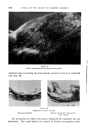
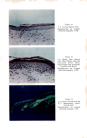
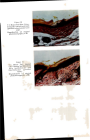
J. Soc. Cosmetic Chemists 15 595-608 (1964) ¸ 1964 Society of Cosmetic Chemists of Great Britain DIFFUSION PROCESSES IN HUMAN HAIR A. W. HOLMES, B.$c., Ph.D.* Presented at the Symposium on "Hair", at Brighton, Sussex, on lSth April 1964. Physical chemistry of diffusion in water and in fibres is considered. The effect of a barrier, containing holes, on diffusion of molecules is applied limited data from which an idea of the size of the holes is obtained. We often alter the appearance or the shape of hair by introducing foreign molecules. Three distinct stages are recognized in this process. In the first stage, molecules are transported to the fibre/water interface by a combination of aqueous diffusion and agitation, if any. The molecules are then adsorbed on to the outer layers of the hair, and in the final stage they diffuse into the hair where they may or may not subsequently participate in reactions with the hair or with themselves. The final stage, again, has three controlling factors: The diffusion of the molecule, the affinity, i.e. the difference in chemical potential of the molecules in solution and the molecules in the hair, and the number of available reactive sites in the hair. Here we are primarily concerned with the process of diffusion within the hair, a process which presents rather special problems and which, in many processes, for instance permanent waving (1) and hair dyeing, is the rate- controlling factor. Diffusion in water has been extensively studied, but much less is known about diffusion in fibres, particularly human hair. The diffusion constant (D) within a substrate is usually defined using Fick's first equation which for unidirectional diffusion, is dc J =- D d-• (1) dc where J is the flux and •xx is the concentration gradient. A second equation is easily derived from the first by considering the rate of accumulation of diffusant within a given element of volume of the substrate, which has the general form dc d (D d•x ) d-• = d-• (2) * Unilever Research Laboratory, Isleworth, Middlesex. 595

596 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS The diffusion constant can be derived from the familiar Stokes-Einstein relationship RT D • -- ($) 6=•r•N where v is the viscosity of the medium, and r• is the molecular radius. This has been shown to hold for spherical particles. Hence it is possible to determine the effective radius of a spherical particle from a knowledge of the diffusion constant, and the viscosity of the solute. Dyestuffs will, in general, not be spherical. Calculations (2) have been made which account for the diffusion of ellipsoids of revolution, which perhaps provides a more satis- factory analogy. For an elongated ellipsoid of axial ratio e (e 1), we have f• (1 -- e•) '• fs e '• In 1 d- (1 --e•) • (4) where f• is the determined frictional coefficient and fs is the frictional coeffi- cient of a sphere of the same volume, and for an oblate ellipsoid (• 1), we have f• (e • -- 1)• f• = e• + tan-• (e •-- 1)• (•) A typical small dye such as acid alizarin black R may be imagined to fulfil either condition. The formula is OH SOaH OH NOs If one allows free rotation about the azo-bond, the molecule approximates to an ellipsoid of axial ratio 1.5. Substituting in the formula above, one has f• --= 1.01. This is sufficiently close to 1 to disregard the effect. Alterna- f• tively one can imagine that the axes are the complete cross section of the molecule and also the depth. Then e --• 4, and we have f• = 1.16. In this f• case, there is a possibility of error which may be as much as 20%. If aggregation of the dye molecules occurs, one would reasonably expect an apparent increase in the radius and hence a lower diffusion constant. If one imagines dimerization with the plain faces of the molecule parallel and close