DIFFUSION PROCESSES IN HUMAN HAIR 597 to each other, we probably have no change in the effective size if the molecule is regarded as an elongated ellipsoid, the extra bulk being compensated for by the decreased freedom of movement. With an oblate ellipsoid, however, f• the axial ratio will decrease by a factor of 2, so we have-• = 1.04 thus, it is a better approximation to a sphere. If this is the case and two planar molecules aggregate in this way, the effective radius will increase by a factor of 1.13, not 1.26 which will occur with the doubling of a sphere. It is doubtful if this could be detected by our present methods, but since the diffusion constant is only reduced by some 10%, it is probably of minor importance in simple diffusion into hair. It may, however, be important if size is a limiting factor. Because of doubt about the behaviour of dyestuffs, the effect of shape will be ignored in subsequent discussion. If the same principles apply to diffusion in hair as to diffusion in water, it should be possible to determine values of D in both media, and hence determine the apparent viscosity of the water in hair. If a barrier is suddenly encountered at a particular molecular size, the apparent viscosity should suddenly increase. Many years ago, Hill (3) solved Fick's second law for infinitely long uniform cylinders in an infinite bath, and obtained a solution of the form Ct Coo -- 1 -- Ae-BK __ Ce-EK (6) Dt where A, B, C and E are constants of known value, K -- a2, and C t and Coo are uptake at times, t and oo. Hill calculated values of cC---•tm for varying values of K, so it is possible to determine values of D from a know- ledge of the uptake/time curve and the radius. This equation gives reason- ably constant values for D, with certain dyes taken up on to cellulose. Crank has developed these ideas for the state where the molecule diffusing into the fibre takes part in rapid irreversible reaction (4), computing values of (•Dt') • for three values of Ct and four values Ofc•. He showed that X, a2,/ Coo a 2 -- 4 C• 1 -• 2 In r--t-- 1 (Z) a where S is the number of reactive sites per unit volume within the fibre, and C B is the number of molecules of solute per unit volume of solution, and r t gives the position of the advancing front at time, t, so that it is possible to

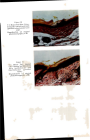
598 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS pt take Crank's data and plot values of a•-for varying values of at three values of C•' One then obtains the straight lines shown in Figure 1. For large reactivity ratios, considerable errors are introduced in the determined values of D if the reactivity is ignored. The values of D reported below have been calculated using Crank's data. 1.2- 1'¸ 04- Figure 1 Dt The effect of reactivity ratio on•-/- at various degrees of uptake (after Crank) A more simple approach to the problem is the familiar plot of dye uptake against (t)( It is easily shown that Ct (_.•)• 2 (s) This equation again assumes an infinite homogeneous cylinder (or slab) in an infinite bath. A plot of C t against (t) • should pass through the origin, but must be expected to deviate from linearity at long times when the bath is becoming depleted or, more important, the curvature of the cylinder becomes significant. Skinkle (5) has attempted to show that the fit of the curve is simply fortuitous and is a reflection of the different behaviour of fibres within the bath, and he suggests that some of the initial assumptions are incorrect. Many plots of dye uptake against (t) • do have linear portions over a much greater distance than one would expect, but with wool and hair they seldom, if ever, pass through the origin. Medley and Andrews (6) have attempted to explain this on the basis of a resistant surface membrane, and claim to provide a more satisfactory fit.