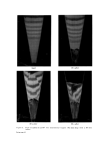
54 JOURNAL OF THE SOCIETY OF COSMETIC CHEMISTS (1) with bin design and predicting how the material will behave during storage. (2) with ensuring an adequate flow of material, and {3) with controlling the flmv at some desired rate. STORAGE HOPPER DESIGN When bulk solids stored in hoppers are allowed to run out under gravity alone, the flow can be mass flow or non-mass flow. In mass flow the bulk solid moves down the vertical portion of the hopper as a solid mass with no relative movement between the particles the top surface retains its original configuration. The material slides over the walls of the hopper in preference to sliding over itself at a place remote from the walls. The effect is to establish a first in--first out flow. In non-mass flow, on the other hand, the material fails and slides over itself the top surface indents and flow takes place by the upper layers funnelling into the centre and then down to the orifice in a moving core. In this type of flow the first material in is not necessarily the first out and, depending on the properties of the material, a proportion of it can remain in the hopper. Segregation of particle sizes also occurs on discharge from non-mass flow hoppers, the components of a mixture segregating by rolling down the free surface at the top of the funnel. It is therefore not advisable to use non-mass flow hoppers for storing mixtures that have a tendency to segregate. A summary of the differences between non mass flow and mass flow hoppers is given in Fig. 1. The effects of segregation have been reported by Davis {1) and by Van Denburg and Bauer (2). The problem has also been discussed by Zenz and Othmer {3) who gave details of the methods that can be used to prevent segregation on filling and discharging hoppers. Johanson {4) has recently described a method of fitting conical inserts in non-mass flow hoppers to prevent segregation and excessive funnelling. Largely due to the pioneering work of Jenike (5} and that of others (t3-9) it is now possible to design mass flow hoppers that flow when the orifice is opened. These methods allow the angle of the hopper cone to be selected to ensure that mass flow takes place and the orifice size to be selected so that it is larger than the maximum size of arch the material can support under the conditions existing at the orifice. J enike's approach to the design of a mass flow hopper was to assume that the material in the converging section of a hopper is a plastic solid. By considering the material to be homogeneous and continuous he was able to

THE FLOW OF PARTICULATE MATERIALS FROM HOPPERS NON- MASSFLOW MASSFLOW SEGREGATION AS MATERIAL ROLLS DOWN SURFACE RELATIVELY HIGH PERCENTAGE OF COARSE IN DI•:HARGE TO P SURFACE REHALEV MIXING \ / oCCURS .,,l -- SECTION ::,'•: ,:,? HATERIAL LEFT IN HOPPER LOADING ORDER NOT ON DISCHARGE ,•SERVED Figure 1. HOPPER EMPTIES COMPLETELY LOADING ORDER PRESERVEO ON DISCHARGE Mass flow and non-mass flow, formulate a set of equations describing the conditions. For the material equations he turned to soil mechanics in which it had been established that when a particulate material is in continuous yield it behaves as a Coulomb solid, i.e. one in which the frictional relationship between shear stress and normal stress is a straight line. It is then possible to describe the material by an angle--the effective angle of friction--under the stress conditions present at the point under consideration. The boundary equation was obtained in a similar way. By the definition of mass flow the material is moving over the walls of the channel which are the boundaries and the