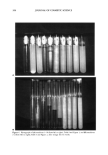
MODEL FRAGRANCE EMULSION SYSTEM 213 The volume of the sedimented part of the emulsion may be estimated from the height of the sediment because the fraction of oil remains constant with the location, as has been shown by Pinfield et al. (20). Hence, a plot of sedimented volume should be linear versus time, as shown in Figure 7A-C. Summarizing equation 2 V = 2•Apg/9qq (Eq. 3) -- the volume sediment is shown to be linear versus time and r 2 may be calculated. Table III shows a good agreement between these droplet sizes and those measured in the photos. The extremely low stability of sample 4 is understood against the colloidal structure of the oil phase (Table III). This emulsion is in fact a "double emulsion" it is a (water-in-oil microemulsion)-in-water system, (W/O l•em)/W (Figure 8). It contains maximum solu- bilized water, i.e., maximum concentration of inverse micelies (or W/O microemulsion droplets), and the exchange of surfactants between the microemulsion droplets and at the O/W (or more precisely W/O microemulsion/water [W/O l•em]/W) interface is facili- tated. Little stability against coalescence may be expected from such an emulsion. The stabilizing action on this emulsion by the liquid crystalline phase is significant, as demonstrated by Figure 4B. The presence of a liquid crystalline phase in samples 5-10 is obvious from the photographs in Figure 9, which was taken against a diffuse light source with the samples placed between crossed polarizers. The birefringence is con- spicous in sample 5 (a thin layer) and in samples 6-8, but weaker in the two last samples. Unfortunately, there is no information about these structures at present. The matter will be resolved in future investigations. Emulsion stabilization by a lameliar liquid crystal is well known (21), but the mecha- nism is not completely understood. It has been referred to as a liquid crystal network influencing the rheology of the continuous phase (22), a discontinuity in the dependence of the Van der Waals attraction forces in the flocculation process (23), the stabilization by vesicles (24,25), and the wedge effect (26). In the present case, the final explanation has to be deferred until information has been obtained about the colloidal structure of emulsions c-h in Figure 4. Figure 10 shows approximately 50% of the total dispersed mass to be liquid crystalline in order to avoid phase separation within a few weeks. It is of some interest that the volume of the creamed emulsion part in Figures 4B and 10 lends itself to a fractal approach. We assume that the emulsion is stable because the liquid crystal focuses on the interconnecting network, iramobilizing the structures. The aqueous space between the connecting liquid crystal particles is characterized as voids, also connecting. Furthermore, assuming that the voids are separated by liquid crystal pathways one has (27,28) Lvoi d oc M 1/dr (Eq. 4) or M o• (Lvoid) df (Eq. 5) in which M is the mass, L is a characteristic length, and df is the fractal dimension.

214 JOURNAL OF COSMETIC SCIENCE 0.3 0.1 0.9 0.8 0.7 0.6 0.5 0.0 " ' 0 A i i I , I [ I , I , I 10 20 30 40 50 Time (min) i i 0.9 0.8 ,,• 0.7 0.6 0.,5 0.4 0.3 0.2 C.! 0.0 2 , I , 6 Time (hour) I i I 8 10 12 1.6 1.4 .• 1.0 • o.• •'• (3.6 0.2 oo o 20 40 60 C Time (rain) 80 100 Figure 7. Sedimentation or creaming volume of ennuisions versus time. A: Emulsion 1' B: Emulsion 2 C: Ennuision 4.