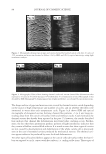
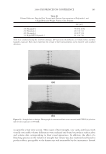
2008 TRI/PRINCETON CONFERENCE 161 designed for goniophotometric measurement and mathematical decomposition, with the polarization decomposition can lead to results that are not correlated to the visual luster sensation. This is especially the case for very dark hair. The most obvious and problematic example with the previous formulae is for treatments on very dark hair. For instance, shine treatments will provoke an important visual increase of luster, with the treated hair tress appearing to have more to much more luster than the same untreated sample according to most panelists (the results are detailed further in the article). In the case of our study, slightly more luster means less than 30% increase, more luster means about 50% more luster and much more luster means about or more than twice as much (100%). However, the increase observed with the Reich Robbins and TRI formulae is moderate, only respectively of 16% and 27%. In some cases, usual formulae may only observe a few percents of increase while the visual difference is obvious. This shows that the luster for- mulae used with polarization have a highly decreased sensitivity to luster changes for very dark hair. We investigated the cause of this lack of sensitivity. For very dark hair, the dif- fused light is extremely low. As a matter of fact, even at the very edge of the distribution (high angles), the specular light is still higher than the diffused light. Considering the true polarimetric diffused light is not relevant in the case of very dark hair, for which the diffused light is negligible in front of the residual specular light located far from the specular peak. This is what causes the lack of sensitivity when the previous formulae are used with the true specular and diffused light measured with polarization. To keep a good sensitivity even when the diffused light is negligible, a new luster formula has been de- veloped (Equation 2), named LBNT (BNT for Bossa Nova Technologies). In this formula, the specular light is split into: O Sin, that corresponds to the peak of the specular light and contributes to increasing the luster. O Sout, that corresponds to the wings of the specular light (high angles) and contributes to decreasing the luster. L Sin D S BNT out visual = + ∗W ( ) (2) Equation 2. New luster formula. The specular light is divided into two components and uses a visual width rather than a width measured on the profi les. This decomposition is made using selection functions and not fi ts. The key to the sensi- tivity of the new luster formula is to choose the good combination of selection functions to obtain a high sensitivity and to measure relative increases that are correlated to the visual sensation. With the new formula, larger increases of luster are observed than with other formulae on dark hair. The observed increases are in the same order of magnitude as the increase observed by panelist. CALCULATION OF Sin Several types of selection function can be used to get Sin (Figure 10). The most simple is a rectangle function. The advantage of a rectangle function is that it has a fl at top so it keeps the exact shape of the specular peak. However it has a straight cut at the edges. To avoid this straight cut, Gaussian function can be used. The disadvantage of Gaussian func- tion is the rounded top which makes the shape of Sin different from the specular peak.

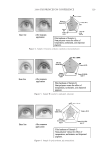
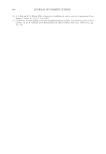
JOURNAL OF COSMETIC SCIENCE 162 The selection function used to isolate Sin in the specular light is a supergaussian function. Supergaussian has a fl at top and no straight cut at the edge and so combines at the same time the advantage of rectangle function and of Gaussian function. It makes physical sense to keep the exact shape of the peak while avoiding straight edges. Other selection function could give better results but the supergaussian has the advantage of being sim- ple while having a physical meaning. This is the reason why the supergaussian has been chosen. A supergaussian function is defi ned by its width and its position. The FWHM (full width half maximum) of the selection function is twice the FWHM of the measured specular profi le. The selection function is centered on the same point as the specular light distri- bution. Then the selection function and measured profi le are multiplied together which gives the Sin signal. The algorithm steps to calculate Sin are summarized below: O Measurement of the maximum value of the specular profi le. O Measurement of the FWHM of the specular profi le and position of the profi le by com- puting the center at the location of the FWHM. The center is not the position of the maximum if the profi le is skewed. Figure 10. The peak of the specular distribution can be selected using different selection functions. (a) Us- ing a rectangle function creates straight edges but the peak selected has the same shape as the specular profi le. (b) Using a Gaussian function does not create straight edges but the peak selected does not follow the same shape as the specular profi le. (c) Using a supergaussian function combines the advantage of rectangle and Gaussian function.