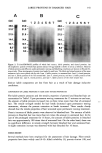
HAIR APPEARANCE AND INTERNAL STRUCTURE 397 hand, the back surface reflection is colored when the object is transparent and colored, because the reflected light passes through inside the object and is partially absorbed by the colorants. The two reflections are, therefore, distinguished from each other by their colors. The visual angle between the two reflections relates directly to the thickness of the model plate, and is one of the cues to depth perception. When the refractive index of this plate is higher than that of the surrounding media, as is generally the case, the visual angle between the two reflections is reduced by refrac- tion, leading to an underestimation of thickness, as shown in Figure 7. This phenomenon is a kind of visual illusion often experienced in daily life when one sees an object in water. If light scattering from the object is strong enough to give an opaque appearance and to significantly reduce the intensity of the back surface reflection, one perceives the front surface reflection and diffused light scattering instead of the back surface reflection, resulting in loss of the sense of depth. The poreless hair shows clear and intensive double reflections with a low level of diffuse scattering, as in Figure 4, so that the poreless hair is evaluated as giving the impression of depth along with transparency. On the other hand, the hair with a porous medulla in Figure 4 shows front surface reflection and diffuse scattering with weak back surface reflection, and then one perceives an opaque impression without an impression of depth in the hair. The color also affects hair appearance in the impression of depth along with transparency, as mentioned above, in terms of the double reflections from the front and back surfaces. When the hair is quite dark (L* 20, that is, almost black), the intensity of the back surface reflection is reduced to a negligible level because of light absorption, and only the front surface reflection is perceived. In such a case, the impression of depth along with transparency is also diminished. INFLUENCE OF CUTICLE STRUCTURE ON VISUAL APPEARANCE The artificial nylon fibers without the cuticle structure in Figure 5b were shown to give an intense luster but also give a metallic, artificial, and flat impression. In contrast, the human hair with a cuticle structure in Figure 5a was perceived to give a natural luster, a colorful appearance, and an impression of depth along with a transparent appearance. This difference in appearance is explained by the models shown in Figure 8. When the surface is flat and the thickness is small like that of the artificial nylon fibers, the visual angle between the front and back surface reflections is nearly zero, as shown in Figure 8a, and the two reflections are overlapped and indistinguishable from each other. It is because the back surface reflection is colored by the color of the object that one perceives the color on the single reflection. On the other hand, when the surface is inclined by the cuticle structure, the front and back surface reflections are separated into opposite directions and the visual angle between the two reflections is enlarged, as shown in Figure 8b. One perceives a clear double reflection, and then an overestimation of thick- ness occurs. Figure 9a shows the visual angle as a function of thickness for flat and inclined surfaces, calculated under the conditions shown in Figure 9b. The visual angle for a flat surface (angle of surface incline: Os -- 0.0 degree) is nearly zero in the region of low thickness

398 JOURNAL OF COSMETIC SCIENCE 8a) Light ('• r '•x View point SOU ce % Reflection from Refiecti/onfrom• Apparent Depth 8b) Light (-•_ source '-•'- • view point 'N", Reflection from ,-N•'".,, Back surface • •) ffl •'""... d .• Visual Reflection from X '•'"- • .f angle Tip ß , Root Apparent Depth ,.' Figure 8. Model illustration to understand light loci from light source to viewpoint via reflections at the front and back surfaces of an object. (a) Thin model with flat surface, and (b) thin model with inclined surface, compared with the models in Figure 7. The inclined surface in (b) corresponds to the cuticle structure of human hair. 9a) 30 • 20 x• Os --_-2.5 degree • Os = 0.0 degree _ • / 0,, o , " 10 ' t .............. • .............. • ............... • ............ 20 ............................................ 0.001 0.01 0.1 1 10 100 • Thickess / cm Order of hair-thic•ess 9b) Geometrical condition for the calculation Light r-• source"•...... Visual \• .... angle.' ! ....................... • ""'. ,.,: 8v . iAngleof } •'"-..Oo , View }surface i \ •".,..,..0.% •,•... point i incline: : \ 5" ...... ..,, • Model Plate \ • ntcgness Point A Figure 9. (a) Thickness dependence of the calculated visual angle of the model plate described in Figure 8. (b) Geometrical condition for the calculations. The vertical axis in (a) shows the visual angles of the back surface reflection against the front surface reflection. The horizontal axis is the thickness of the model plate. The solid lines with closed circles and open circles, and the dotted line with closed circles, in Figure (a) are for Os = -2.5 degrees, 0.0 degree, and 2.5 degrees, respectively, where Os is the angle of surface incline defined in (b). In the geometrical condition for the calculation, the following four parameters are fixed, as in (b): (1) The refractive indexes of the model plate and the surrounding media are 1.5 and 1.0, respectively. (2) The distance between the viewpoint and the model plate (viewpoint to point A in the figure) is 30 cm. (3) The distance from the light source to point A is 100 cm. (4) The angle between (2) and (3) above at point A is 45 degrees. for inclined surfaces (0s = 2.5 or -2.5 degrees), however, it stays at a finite value even in the extremely thin region. In the case of human hair showing clear double reflections, the impression of depth along with transparency is perceived, as described in the previous section. On the other hand,