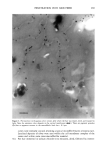
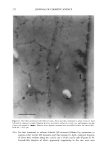
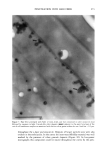
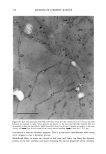
ELEMENTAL DISTRIBUTION IN HAIR 307 enhancement of fluorescent lines by other fluorescent lines of higher energy, can be applied in the "fundamental parameter model." This model takes into account all factors contributing to the result in XRF measurements and calculates the result in terms of relevant concentrations. The calculations are simpler for X-rays than for ion beams, and several programs of this type exist, usually provided by the X-ray equipment manufac- turers. The programs generally use standards for calibration but calculate the concen- trations of the detected elements in the sample using data on primary beam, sample, detector, distances, etc. Overlap of peaks, e.g., Cu K= and Zn K=, is handled by the program used in this work, as a comparison with the known relations between K= and K• peaks for each element, taking the energy distribution of the primary beam into account together with energies of all peaks. A mathematical algorithm fits a function to the peaks and background in the spectrum to determine peak areas and energies. In practice, this allows quantitative evaluation of data to be a straightforward computer- assessed task. In the development of physical methods to be applied to biological materials, repro- ducibility is one of the crucial factors. Local factors, such as the mineral content of drinking water and individual differences in food product uptake, will be mirrored in the trace-element content of the individual body and its tissues. The biological variation of elemental content is generally a heavily influencing factor on reproducibility when a biological material is analyzed for minerals and trace elements. This effect is clearly seen in the present investigation as different degrees of reproducibility evident for different elements, e.g., monovalent ions versus divalent ones. Most Caucasian hair fibers are more or less elliptical in cross section (17). Hence one factor that may influence the analysis of single fibers is the effective diameter of the fiber in the X-ray beam. Rotating the fiber through a defined set of angles, it can be seen that Zn shows the least tendency of variation, whereas Ca and especially S are variable (Figure 3). To a large extent this can be explained by an absorption effect due to the compar- atively low energy of the fluorescent Ca and S X-ray photons, which will be more attenuated when the long axis of the ellipsoid cross section is directed towards the detector (Figure 3b) than when the ellipsoid has an orientation corresponding to a shorter pathway through the hair matrix material. For the heavier elements, i.e., higher X-ray fluorescence energies, this attenuation effect becomes less pronounced. The effects for sulfur and chlorine are about + 15% for 0.030 mm hair diameter and - 15% fbr 0.060 mm hair diameter, respectively, compared to the diameter value used for calculations of concentrations. Because of this large variation with diameter, the data from these ele- ments have low precision. Potassium and calcium signals are absorbed up to about + 10%, and for Cu the effect is less than +2% for the hair diameters 0.030 mm and 0.060 mm (assuming a hair diameter of 0.045 mm). To a certain, probably smaller, extent, the grade of ellipticity also affects these results. The long-term reproducibility study reflects variations in the analytical qualities of the instrument as well as variations in the analyzed region of the hair fibers. The hypothesis that it mainly reflects variations along the hairs is supported by the fact that there is no strong tendency of co-variation in the measurements. A homogenous sample used in the same manner would have provided a measure of the instrumental stability. The longitudinal distribution of an element in a hair fiber reflects to a certain extent how tightly bound this element is to the organic matrix of the fiber, i.e., how much its

308 JOURNAL OF COSMETIC SCIENCE concentration will be influenced by the degree of re-distribution, extraction, and/or contamination from the environment, cosmetic and hygienic effects included. In our study such variations appear to lie within expected biological variation limits for Cu, whereas K increases conspicuously above a position approximately 2 mm from the root (position 10), further emphasizing the necessity that hair analyses shall be confined to the virgin part of the hair fiber. A similar distribution pattern is also evident for Ca, which is an expected contaminant through its general presence in (tap) water. The stability of the concentration of Cu gives further support to the idea that Cu and Zn are better choices for internal standard reference than S in semi-quantitative analyses (11). However, tap water and pool water may contain appreciable amounts of Cu 2+, which may bind strongly to the hair fiber, especially if the water is chlorinated (22). The best candidate for an internal standard is therefore Zn. In this work, an analytical time of twelve minutes was chosen for each hair. This was a reasonable compromise between efficiency of work and precision in the measurement of elements present at low concentrations. It is difficult to make sure that a hair fiber is completely free from contaminants on the surface. To be reasonably confident, reanalyses of all measurements, with cleanings in between, should be performed for a comparison of the results. Such measurements are beyond the scope of the present investigation. However, reproducibility tests and the performed reanalyses of hairs with high levels of some elements show that the problem is not a severe one, albeit existing. In addition to the endogenous variation in elemental content expected from a biological sample, there are effects of measurement variations due to contamination and the intrinsic variability of the physical measurement system. In hair analysis the contamination appears to be the most serious problem. To minimize the effects of extreme data values, we have used the empirical median value for each individual (three or six hairs) in computation of elemental content (Table II). No significant discrepancies between the washed and unwashed hairs were observed. Ex- treme values in some fibers are especially obvious in the cases of K and Ca, elements that can be redistributed and extracted by contact with water. Ordinary tap water used for hygienic and cosmetic purposes, in addition, may contaminate the hair. However, with three or six independent measurements (corresponding to the number of analyzed hair fibers from each person), incorrect data from single measurements will not affect the calculated median values for each person (Table II). Calculation of concentrations has been made based on the assumption of a hair diameter of 0.045 mm. An actual diameter below this value results in an overestimation when calculating the concentrations, especially for the lighter elements like S and C1. In fact, the diameter will have strong influence on the measurement of these elements due to the attenuation the characteristic X-rays undergo in the hair bulk material (9). For higher energy characteristic lines, and for the intensity of scattered radiation, this attenuation effect becomes negligible as compared to other variations of biological material. Since the actual diameter of each hair fiber has not been measured, a discrepancy in measured data compared to the true values is likely to exist. Furthermore, the calculations assume an even distribution over the cross section, which is not true for many of the elements (2,6,15), and this will also affect the results to some extent, again especially for light elements (18). Reproducibility is of crucial importance in hair analysis for diagnosis of illness or in