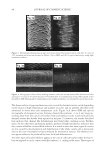
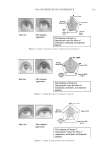
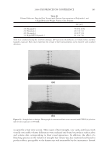
JOURNAL OF COSMETIC SCIENCE 160 The four most used formulae are the Reich-Robbins, TRI, Stamm and Guiolet formulae (Equations 1). Among these, Reich-Robbins and TRI formulae are the most used. For instance, Reich-Robbins is the direct mathematical translation of the three basic assess- ments about Luster. Reich-Robbins Luster is directly proportional to the amount of spec- ular light S, so a two-fold increase of specular light results in a two-fold increase of Luster. It is also inversely proportional to the amount of diffused light, so if the background light is two times darker, the luster is two times greater. Finally, it is also inversely proportional to the angular width of the distribution so if the specular light width is divided by two, the specular light is twice as concentrated and the luster is two times greater. The TRI formula is similar to the Reich-Robbins one except that the diffused light is replaced by the specular plus the diffused light and that the luster is normalized by a reference angle. Stamm and Guiolet do not take into account the angular width of the distribution. L Re ich S D * −Robbins = 1/2 θ L TRI ref S S D = + θ θ 1 2 / (1) L S D S Stamm = − L Guiolet S D = Equations 1. The four most used luster formulae are the Reich-Robbins, TRI, Stamm and Guiolet formulae. USE OF PREVIOUS LUSTER FORMULAE WITH POLARIZATION DECOMPOSITION The previously described luster formulae were designed with mathematical separations of specular and diffused light (curve fi tting and other deconvolution methods). They give results that are well correlated to the visual perception with goniophotometric measurements. They can also be calculated with the physical separation of diffused and specular light distribution obtained with polarization. However, using these formulae, that were Figure 9. Luster is considered to depend on three parameters. (a) Increase of the amount of light refl ected. (b) Reduction of the width of the specular light while keeping the overall amount of specular light constant, so light is more concentrated for a smaller width. (c) Increase of the diffused light (background) while keep- ing the refl ected light the same.

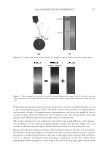
2008 TRI/PRINCETON CONFERENCE 161 designed for goniophotometric measurement and mathematical decomposition, with the polarization decomposition can lead to results that are not correlated to the visual luster sensation. This is especially the case for very dark hair. The most obvious and problematic example with the previous formulae is for treatments on very dark hair. For instance, shine treatments will provoke an important visual increase of luster, with the treated hair tress appearing to have more to much more luster than the same untreated sample according to most panelists (the results are detailed further in the article). In the case of our study, slightly more luster means less than 30% increase, more luster means about 50% more luster and much more luster means about or more than twice as much (100%). However, the increase observed with the Reich Robbins and TRI formulae is moderate, only respectively of 16% and 27%. In some cases, usual formulae may only observe a few percents of increase while the visual difference is obvious. This shows that the luster for- mulae used with polarization have a highly decreased sensitivity to luster changes for very dark hair. We investigated the cause of this lack of sensitivity. For very dark hair, the dif- fused light is extremely low. As a matter of fact, even at the very edge of the distribution (high angles), the specular light is still higher than the diffused light. Considering the true polarimetric diffused light is not relevant in the case of very dark hair, for which the diffused light is negligible in front of the residual specular light located far from the specular peak. This is what causes the lack of sensitivity when the previous formulae are used with the true specular and diffused light measured with polarization. To keep a good sensitivity even when the diffused light is negligible, a new luster formula has been de- veloped (Equation 2), named LBNT (BNT for Bossa Nova Technologies). In this formula, the specular light is split into: O Sin, that corresponds to the peak of the specular light and contributes to increasing the luster. O Sout, that corresponds to the wings of the specular light (high angles) and contributes to decreasing the luster. L Sin D S BNT out visual = + ∗W ( ) (2) Equation 2. New luster formula. The specular light is divided into two components and uses a visual width rather than a width measured on the profi les. This decomposition is made using selection functions and not fi ts. The key to the sensi- tivity of the new luster formula is to choose the good combination of selection functions to obtain a high sensitivity and to measure relative increases that are correlated to the visual sensation. With the new formula, larger increases of luster are observed than with other formulae on dark hair. The observed increases are in the same order of magnitude as the increase observed by panelist. CALCULATION OF Sin Several types of selection function can be used to get Sin (Figure 10). The most simple is a rectangle function. The advantage of a rectangle function is that it has a fl at top so it keeps the exact shape of the specular peak. However it has a straight cut at the edges. To avoid this straight cut, Gaussian function can be used. The disadvantage of Gaussian func- tion is the rounded top which makes the shape of Sin different from the specular peak.