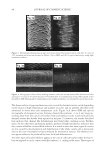
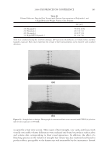
JOURNAL OF COSMETIC SCIENCE 162 The selection function used to isolate Sin in the specular light is a supergaussian function. Supergaussian has a fl at top and no straight cut at the edge and so combines at the same time the advantage of rectangle function and of Gaussian function. It makes physical sense to keep the exact shape of the peak while avoiding straight edges. Other selection function could give better results but the supergaussian has the advantage of being sim- ple while having a physical meaning. This is the reason why the supergaussian has been chosen. A supergaussian function is defi ned by its width and its position. The FWHM (full width half maximum) of the selection function is twice the FWHM of the measured specular profi le. The selection function is centered on the same point as the specular light distri- bution. Then the selection function and measured profi le are multiplied together which gives the Sin signal. The algorithm steps to calculate Sin are summarized below: O Measurement of the maximum value of the specular profi le. O Measurement of the FWHM of the specular profi le and position of the profi le by com- puting the center at the location of the FWHM. The center is not the position of the maximum if the profi le is skewed. Figure 10. The peak of the specular distribution can be selected using different selection functions. (a) Us- ing a rectangle function creates straight edges but the peak selected has the same shape as the specular profi le. (b) Using a Gaussian function does not create straight edges but the peak selected does not follow the same shape as the specular profi le. (c) Using a supergaussian function combines the advantage of rectangle and Gaussian function.

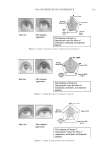
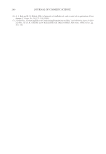
2008 TRI/PRINCETON CONFERENCE 163 O From the FWHM and position of the profi le, the selection function is calculated. O Selection function and profi les are multiplied to get Sin signal. These steps are summarized in Figure 11. CALCULATION OF Sout The selection function to isolate Sout is of the form 1-supergaussian. Many types of super- gaussian functions have been tested to obtain the best sensitivity. The simplest solution would have been to take all the light that was not considered to be part of Sin. However, we observed that this leads to relatively moderate increase sensitivity. This is caused by the intermediate part between the wings and the peak of the specular profi le which has a behaviour close to the one of the peak and dominates the Sout signal as it contains much more light that the far wings. After testing several cases, it was observed that the sensitiv- ity was increased when Sout was taken further from the specular peak. In this case, some of the specular light is considered neither in Sin nor in Sout. As Sout is observed only in the wings while the diffused light is observed for all the angles, the ratio of Sout and the Figure 11. Extraction of Sin from the specular profi le. The selection function is calculated (b) with the pa- rameters computed (a) from the specular light distribution. Multiplying the selection function and the spec- ular light profi le gives the Sin profi le (c).