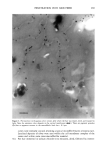
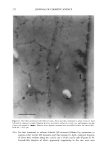
306 JOURNAL OF COSMETIC SCIENCE Table II Elemental Content of Hair Fibers in a Normal Caucasian Population (n = 20), Given in pg/g Element Median Mean +/- 1S.D. Minimum Maximum Unit S 3.6 3.6 0.5 2.0 4.6 % CI 0.5 0.5 0.1 0.2 1.0 % K * 78 195 * 1261 pg/g Ca 186 194 92 53 507 pg/g Fe 2 3 3 * 18 ktg/g Cu 4 5 2 1 18 pg/g Zn 183 182 17 148 232 pg/g * Data below the detection limit. The data were calculated from the emprical median values of the hair fibers obtained from each individual. As in Table I, elements with a skew distribution have conspicuous differences between empirical median and empirical mean values, cf. K and Ca versus Zn. It is conceivable that physiologically important elements are more or less effectively trapped by bonding to proteins in the consolidated fiber. In consequence, the overall elemental composition will reflect the status of the particular hair follicle at growth. Longitudinal studies of the elemental distributions in hair follicles support this tentative argument (2). Moreover, interference due to contamination and extraction imposed on the fiber by the environment (including any cosmetic activity) complicates the analysis (cf. refs. 5,14). Analyzing a virgin part of the hair fiber, i.e., the first few (2-5 mm) millimeters will provide the information sought for with minimal contamination. The sampling area on the scalp is important because individuals with a heredity for AnA (androgenetic alopecia) may in fact have a conspicuously increased number of telogen follicles in the coronal and frontal areas long before the typical pattern of hair loss becomes obvious (3). The region chosen in this study, the temporal one, is excluded from the AnA type of hair loss and represents an area with a normal anagen/telogen ratio of hair follicle distribution. It may be noted that different areas of the scalp may indeed reveal different elemental contents, as was demonstrated by Seta et M. (24). No methods are truly inert, and some, e.g., the particle probes (XRMA, PIXE), will, in the course of prolonged times of analysis, cause a "burn-out" of the light and volatile elements (mainly H, C, N, O) in the organic matrix of a biological sample. This will result in a change of the (non-volatile) metal element to background ratio, and appar- ently higher-than-live concentrations of such elements will be recorded. The effect is time-dependent and may exist also for the X-ray fluorescence (XRF) technique. How- ever, using X-ray excitation of characteristic X-rays, the samples are virtually unaffected with doses of the magnitude used in this study. Revisits to the same area of analysis will thus be meaningful in terms of reproducibility. ITRAX, the instrument used in the present study, represents a new design for trace- element analysis in small samples. The high sensitivity of the instrument is achieved by a specific combination of properties, namely monochromacy of the primary beam and high intensity due to the high-efficiency capillary focusing device. Comprehensive de- scriptions of the technique have been published (7,16,21). In XRF, all-important phenomena contributing to the result of the analysis, e.g., attenuation of the primary beam or the fluorescent beam and any secondary effects like

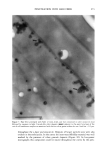
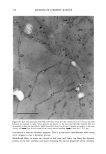
ELEMENTAL DISTRIBUTION IN HAIR 307 enhancement of fluorescent lines by other fluorescent lines of higher energy, can be applied in the "fundamental parameter model." This model takes into account all factors contributing to the result in XRF measurements and calculates the result in terms of relevant concentrations. The calculations are simpler for X-rays than for ion beams, and several programs of this type exist, usually provided by the X-ray equipment manufac- turers. The programs generally use standards for calibration but calculate the concen- trations of the detected elements in the sample using data on primary beam, sample, detector, distances, etc. Overlap of peaks, e.g., Cu K= and Zn K=, is handled by the program used in this work, as a comparison with the known relations between K= and K• peaks for each element, taking the energy distribution of the primary beam into account together with energies of all peaks. A mathematical algorithm fits a function to the peaks and background in the spectrum to determine peak areas and energies. In practice, this allows quantitative evaluation of data to be a straightforward computer- assessed task. In the development of physical methods to be applied to biological materials, repro- ducibility is one of the crucial factors. Local factors, such as the mineral content of drinking water and individual differences in food product uptake, will be mirrored in the trace-element content of the individual body and its tissues. The biological variation of elemental content is generally a heavily influencing factor on reproducibility when a biological material is analyzed for minerals and trace elements. This effect is clearly seen in the present investigation as different degrees of reproducibility evident for different elements, e.g., monovalent ions versus divalent ones. Most Caucasian hair fibers are more or less elliptical in cross section (17). Hence one factor that may influence the analysis of single fibers is the effective diameter of the fiber in the X-ray beam. Rotating the fiber through a defined set of angles, it can be seen that Zn shows the least tendency of variation, whereas Ca and especially S are variable (Figure 3). To a large extent this can be explained by an absorption effect due to the compar- atively low energy of the fluorescent Ca and S X-ray photons, which will be more attenuated when the long axis of the ellipsoid cross section is directed towards the detector (Figure 3b) than when the ellipsoid has an orientation corresponding to a shorter pathway through the hair matrix material. For the heavier elements, i.e., higher X-ray fluorescence energies, this attenuation effect becomes less pronounced. The effects for sulfur and chlorine are about + 15% for 0.030 mm hair diameter and - 15% fbr 0.060 mm hair diameter, respectively, compared to the diameter value used for calculations of concentrations. Because of this large variation with diameter, the data from these ele- ments have low precision. Potassium and calcium signals are absorbed up to about + 10%, and for Cu the effect is less than +2% for the hair diameters 0.030 mm and 0.060 mm (assuming a hair diameter of 0.045 mm). To a certain, probably smaller, extent, the grade of ellipticity also affects these results. The long-term reproducibility study reflects variations in the analytical qualities of the instrument as well as variations in the analyzed region of the hair fibers. The hypothesis that it mainly reflects variations along the hairs is supported by the fact that there is no strong tendency of co-variation in the measurements. A homogenous sample used in the same manner would have provided a measure of the instrumental stability. The longitudinal distribution of an element in a hair fiber reflects to a certain extent how tightly bound this element is to the organic matrix of the fiber, i.e., how much its